【题目】已知关于x的方程mx2﹣(m+2)x+2=0
(1)求证:不论m为何值,方程总有实数根;
(2)若方程的一个根是2,求m的值及方程的另一个根.
参考答案:
【答案】(1)证明见解析(2)1,1
【解析】
试题分析:(1)分类讨论:当m=0时,方程为一元一次方程,有一个实数解;当m≠0时,计算判别式得到△=(m﹣2)2≥0,则方程有两个实数解,于是可判断不论m为何值,方程总有实数根;
(2)设方程的另一个根为t,利用根与系数的关系得到2+t=![]() ,2t=
,2t=![]() ,然后解关于t与m的方程组即可.
,然后解关于t与m的方程组即可.
试题解析:(1)证明:当m=0时,方程变形为﹣2x+2=0,解得x=1;
当m≠0时,△=(m+2)2﹣4m2=(m﹣2)2≥0,方程有两个实数解,
所以不论m为何值,方程总有实数根;
(2)设方程的另一个根为t,
根据题意得2+t=![]() ,2t=
,2t=![]() ,
,
则2+t=1+2t,解得t=1,
所以m=1,
即m的值位1,方程的另一个根为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a、b互为相反数,c、d互为倒数,x的绝对值是3,求代数式 a+b+x﹣cd的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题呈现:
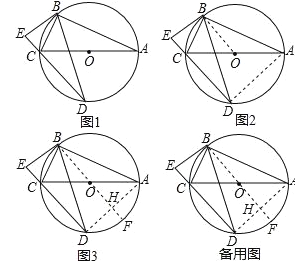
如图1,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BE⊥DC交DC的延长线于点E.求证:BE是⊙O的切线.
问题分析:
连接OB,要证明BE是⊙O的切线,只要证明OB ____ BE,由题意知∠E=90°,故只需证明OB ___ DE.
解法探究:
(1)小明对这个问题进行了如下探索,请补全他的证明思路:
如图2,连接AD,由∠ECB是圆内接四边形ABCD的一个外角,可证∠ECB=∠BAD,因为OB=OC,所以 __ ,因为BD=BA,所以 ______ ,利用同弧所对的圆周角相等和等量代换,得到 ____ ,所以DE∥OB,从而证明出BE是⊙O的切线.
(2)如图3,连接AD,作直径BF交AD于点H,小丽发现BF⊥AD,请说明理由.
(3)利用小丽的发现,请证明BE是⊙O的切线.(要求给出两种不同的证明方法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,各类方程的解法虽然不尽相同,但是它们的基本思想都是“转化”,即把未知转化为已知.用“转化”的数学思想,我们还可以解一些新方程.
认识新方程:
像
 =x这样,根号下含有未知数的方程叫做无理方程,可以通过方程两边平方把它转化为2x+3=x2,解得x1=3,x2=﹣1.但由于两边平方,可能产生增根,所以需要检验,经检验,x2=﹣1是原方程的增根,舍去,所以原方程的解是x=3.
=x这样,根号下含有未知数的方程叫做无理方程,可以通过方程两边平方把它转化为2x+3=x2,解得x1=3,x2=﹣1.但由于两边平方,可能产生增根,所以需要检验,经检验,x2=﹣1是原方程的增根,舍去,所以原方程的解是x=3.运用以上经验,解下列方程:
(1)
 =x;
=x;(2)x+2
 =6.
=6. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面各组数据中,众数是3.5的是( )
A. 4,3,4,3 B. 1.5,2,2.5,3.5
C. 3.5,4.5,3.5 D. 6,4,3,2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在描述一组数据的集中趋势时,应用最广泛的是( )
A. 众数 B. 中位数 C. 平均数 D. 全体数据
相关试题

