【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③.

(1)图②有______个三角形;图③有______个三角形;
(2)按上面的方法继续下去,第n个图形中有_________个三角形(用n的代数式表示).
(3)是否存在正整数n,使得第n个图形中存在2019个三角形?如果存在,请求出n的值;如果不存在,请说明理由。
参考答案:
【答案】(1)5,9;(2)4n﹣3;(3)不存在,理由见解析
【解析】
(1)根据图形的变化可发现每个图形比前一个图形多4个三角形,结合图①有一个三角形即可得出结论;(2)根据图形的变化可发现每个图形比前一个图形多4个三角形,而图形①只有一个三角形,用含n的代数式表示出结论即可;(3)结合(2)的结论,令三角形的个数等于2019,看n的值是否为整数,是的话则第n个图形就是所求,如果不是,则不存在.
解:(1)图②中有5个三角形,图③中有9个三角形.
故答案为:5,9;
(2)依题意得:n=1时,有1个三角形;
n=2时,有5个三角形;
n=3时,有9个三角形;
∴当n=n时,有(4n﹣3)个三角形.
故答案为:4n﹣3;
(3)不存在
假设存在正整数n,
使得第n个图形中有2019个三角形,
根据题意得:4n﹣3=2019,
解得:n=![]() ,不是整数,
,不是整数,
故不存在正整数n,使得第n个图形中有2019个三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
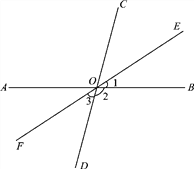
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:

①A、B之间的距离为1200m; ②乙行走的速度是甲的1.5倍;③ b=960; ④ a=34.
以上结论正确的有( )
A. ①② B. ①②③ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在2019个“口”中依次填入一列数字m1,m2,m3;……. m2019,使得其中任意四个相邻的“口”中所填的数字之和都等于-10.已知m4=0,m6=-7,则m1+m2019的值为( )

A.0B.-3C.-10D.-14
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题.

(1)从中取出2张卡片,使这两张卡片上数字的乘积最大,乘积的最大值为______.
(2)从中取出2张卡片,使这两张卡片上数字相除的商最小,商的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两班英语口语水平,每班随机抽取了10名学生进行了口语测验,测验成绩满分为10分,参加测验的10名学生成绩(单位:分)称为样本数据,抽样调查过程如下:
收集数据
甲、乙两班的样本数据分别为:
甲班:6 7 9 4 6 7 6 9 6 10
乙班:7 8 9 7 5 7 8 5 9 5
整理和描述数据
规定了四个层次:9分以上(含9分)为“优秀”,8-9分(含8分)为“良好”,6-8分(含6分)为“一般”,6分以下(不含6分)为“不合格”。按以上层次分布绘制出如下的扇形统计图。

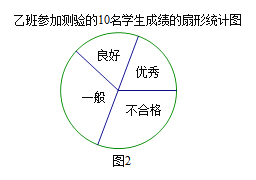
请计算:(1)图1中,“不合格”层次所占的百分比;
(2)图2中,“优秀”层次对应的圆心角的度数。
分析数据
对于甲、乙两班的样本数据,请直接回答:
(1)甲班的平均数是7,中位数是_____;乙班的平均数是_____,中位数是7;
(2)从平均数和中位数看,____班整体成绩更好。
解决问题
若甲班50人,乙班40人,通过计算,估计甲、乙两班“不合格”层次的共有多少人?
相关试题

