【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题.
![]()
(1)从中取出2张卡片,使这两张卡片上数字的乘积最大,乘积的最大值为______.
(2)从中取出2张卡片,使这两张卡片上数字相除的商最小,商的最小值为______.
参考答案:
【答案】(1)40;(2)-2.
【解析】
(1)从中2张卡片,要使这2张卡片上数字的乘积最大,应该取两张同号的,再进行比较即可;
(2)从中抽取2张卡片,要使这两张卡片数相除的商最小,则一个是正数,另一个是负数,且商的绝对值最大,据此求解即可.
解:(1)(+4)×(+5)=20
(-5)×(-8)=40
因为40>20,
所以其中的一个数抽-5,另一个数是-8时,最大值是40.
故答案是:40.
(2)从中抽取2张卡片,要使这两张卡片数相除的商最小,则一个是正数,另一个是负数,且商的绝对值最大,故应取-8和+4,
(-8)÷(+4)=-2
所以其中的一个数抽-8,另一个数是+4时,它们相除即是商的最小值是-2.
故答案是:-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:

①A、B之间的距离为1200m; ②乙行走的速度是甲的1.5倍;③ b=960; ④ a=34.
以上结论正确的有( )
A. ①② B. ①②③ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③.

(1)图②有______个三角形;图③有______个三角形;
(2)按上面的方法继续下去,第n个图形中有_________个三角形(用n的代数式表示).
(3)是否存在正整数n,使得第n个图形中存在2019个三角形?如果存在,请求出n的值;如果不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在2019个“口”中依次填入一列数字m1,m2,m3;……. m2019,使得其中任意四个相邻的“口”中所填的数字之和都等于-10.已知m4=0,m6=-7,则m1+m2019的值为( )

A.0B.-3C.-10D.-14
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两班英语口语水平,每班随机抽取了10名学生进行了口语测验,测验成绩满分为10分,参加测验的10名学生成绩(单位:分)称为样本数据,抽样调查过程如下:
收集数据
甲、乙两班的样本数据分别为:
甲班:6 7 9 4 6 7 6 9 6 10
乙班:7 8 9 7 5 7 8 5 9 5
整理和描述数据
规定了四个层次:9分以上(含9分)为“优秀”,8-9分(含8分)为“良好”,6-8分(含6分)为“一般”,6分以下(不含6分)为“不合格”。按以上层次分布绘制出如下的扇形统计图。

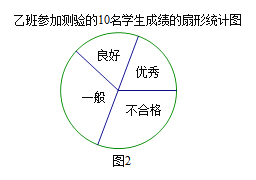
请计算:(1)图1中,“不合格”层次所占的百分比;
(2)图2中,“优秀”层次对应的圆心角的度数。
分析数据
对于甲、乙两班的样本数据,请直接回答:
(1)甲班的平均数是7,中位数是_____;乙班的平均数是_____,中位数是7;
(2)从平均数和中位数看,____班整体成绩更好。
解决问题
若甲班50人,乙班40人,通过计算,估计甲、乙两班“不合格”层次的共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在一条可以折叠的数轴上,点A,B分别表示数-9和4.
(1)A,B两点之间的距离为________.
(2)如图2,如果以点C为折点,将这条数轴向右对折,此时点A落在点B的右边1个单位长度处,则点C表示的数是________.
(3)如图1,若点A以每秒3个单位长度的速度沿数轴向右运动,点B以每秒2个单位长度的速度也沿数轴向右运动,那么经过多少时间,A、B两点相距4个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在相邻两点距离为1的点阵纸上(左右相邻或上下相邻的两点之间的距离都是1个单位长度),三个顶点都在点阵上的三角形叫做点阵三角形,请按要求完成下列操作:

(1)将点阵△ABC水平向右平移4个单位长度,再竖直向上平移5个单位长度,画出平移后的△A1B1C1;
(2)连接AA1、BB1,则线段AA1、BB1的位置关系为 、数量关系为 .估计线段AA1的长度大约在 <AA1< 单位长度:(填写两个相邻整数);
(3)画出△ABC边AB上的高CD.
相关试题

