【题目】有一间阶梯教室,第1排的座位数为a,从第2排开始,每一排都比前一排增加b个座位,
(1)请你在下表的空格里填写一个适当的式子:
第1排座位数 | 第2排座位数 | 第3排座位数 | 第4排座位数 | …… |
a | a+b | a+2b` | …… |
(2)已知第4排有18个座位,第15排的座位数是第5排座位数的2倍,求第21排有多少个座位?
参考答案:
【答案】(1)a+3b;(2)52个.
【解析】分析: (1)由题意可得出,第n排的座位数为a+(n-1)b(n≥1);
(2)中等量关系应为:第5排的座位数×2=第15排的座位数,再根据关键语“第4排有18个座位“,列出方程组,求解.
详解:
(1)a+3b;
(2)根据题意,得![]() 解得
解得![]()
所以12+20×2=52.
答:第21排有52个座位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面对话,可知懒羊羊所买的笔和笔记本的;
价格分别为( )
喜羊羊:懒羊羊,你上周买的笔和笔记本的价格是多少啊?
懒羊羊:哦,我忘了,只记得先后买了两次,第一次买了5支笔和10本笔记本共花了42元钱,第二次买了10支笔和5本笔记本共花了30元钱。
A. 0.8元/支,2.6元/本 B. 0.8元/支,3.6元/本
C. 1.2元/支,3.6元/本 D. 1.6元/支,3.2元/本
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=
 AB中,一定正确的是( )
AB中,一定正确的是( ) 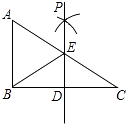
A.①②③
B.①②④
C.①③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为( )
A. 21 B. 15 C. 9 D. 9或21
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )

A.(2017,0)
B.(2017 ,
, 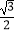 )
)
C.(2018, )
)
D.(2018,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)如图①,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB;


(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,∠DCB=30°,求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
相关试题

