【题目】用两种方法证明“三角形的外角和等于360°”.
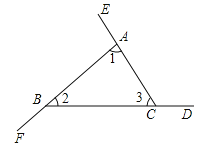
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
参考答案:
【答案】平角等于180°,∠1+∠2+∠3=180°.
【解析】证法1:∵平角等于180°,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
证法2:∵∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),∵∠1+∠2+∠3=180°,∴∠BAE+∠CBF+∠ACD=360°.
故答案为:平角等于180°,∠1+∠2+∠3=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣4x﹣5=0时,原方程应变形为( )
A.(x+1)2=6B.(x+2)2=9C.(x﹣1)2=6D.(x﹣2)2=9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)、求证:DE⊥AG;
(2)、如图2,正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°),得到正方形OE′F′G′;
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为2,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
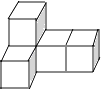
A.主视图的面积最小
B.左视图的面积最小
C.俯视图的面积最
D.三个视图的面积相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴上有A、B、C、D四个点,分别对应的数为a、b、c、d,且满足a=﹣2,|b|=0,(c﹣12)2与|d﹣18|互为相反数.
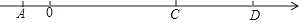
(1)b=;c=;d= .
(2)若A、B两点以2个单位长度/秒的速度向右匀速运动,同时C、D两点以1个单位长度/秒的速度向左匀速运动,并设运动时间为t秒,问t为多少时,A、C两点相遇?
(3)在(2)的条件下,A、B、C、D四点继续运动,当点B运动到点D的右侧时,问是否存在时间t,使得B与D的距离是C与D的距离的3倍?若存在,求时间t;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数
B.点数的和为奇数
C.点数的和小于13
D.点数的和小于2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线
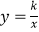 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 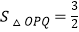 ,则k的值是( )
,则k的值是( )
A.4
B.2
C.
D.
相关试题

