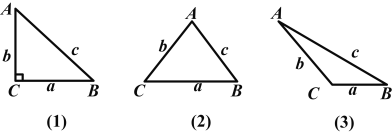
【题目】在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),则根据勾股定理,得a2+b2=c2.若△ABC不是直角三角形,如图(2)和(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
参考答案:
【答案】见解析
【解析】
解:若△ABC为锐角三角形,则有a2+b2>c2,若△ABC为钝角三角形,∠C为钝角,则有a2+b2<c2.
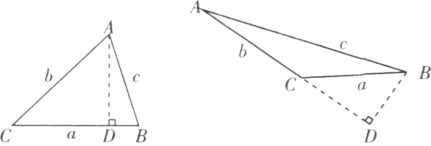
证明:(1)当△ABC为锐角三角形时,过点A作AD⊥CB,垂足为D,设CD=x,则有DB=a-x.
根据勾股定理,得b2-x2=c2-(a-x)2,即b2-x2=c2-a2+2ax-x2.
∴a2+b2=c2+2ax.∵a>0,x>0,∴2ax>0,
∴a2+b2>c2.
(2)当△ABC为钝角三角形时,过B作BD⊥AC,交AC的延长线于点D,设CD=x,则BD2=a2-x2.根据勾股定理,得(b+x)2+(a2-x2)=c2,∴a2+b2+2bx=c2.
∵b>0,x>0,∴2bx>0,∴a2+b2<c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是( )
A.不断变大
B.不断减小
C.不变
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=
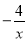 (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.(1)求直线l的解析式;
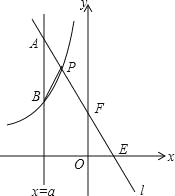
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的腰长为10,一腰上的高为6,则以底边为边长的正方形的面积为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某军事行动中,对军队部署的方位,采用代码的方式来表示.例如,北偏东30°方向45km的位置与钟面相结合,以钟面圆心为基准,时针指向北偏东30°的时刻是1∶00,那么这个地点就用代 码010045表示.按这种表示方式,南偏东40°方向78km的位置,可用代码表示为..
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,不是中心对称图形的是( )
A.平行四边形
B.圆
C.正八边形
D.等边三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知m是方程式x2+x﹣1=0的根,则式子m3+2m2+2019的值为_____.
相关试题

