【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去租用这两种货车情况如下:
第一次 | 第二次 | |
甲种货车数量 | 2辆 | 5辆 |
乙种货车数量 | 3辆 | 6辆 |
累计运货重量 | 14吨 | 32吨 |
(1)分别求甲、乙两种货车载重多少吨?
(2)现在租用该公司5辆甲货车和7辆乙货车一次刚好运完这批货物,如果按每吨付费50元计算,货主应付运费多少元?
参考答案:
【答案】
(1)解:设甲种货车每辆载重x吨,乙种货车每辆载重y吨,则
![]() ,
,
解之得 ![]() .
.
答:甲种货车每辆载重4吨,乙种货车载重2吨
(2)解:4×5+2×7=34(吨),34×50=1700(元).
答:货主应付运费1700元
【解析】(1)设甲种货车每辆载重x吨,乙种货车每辆载重y吨,然后依据2辆甲种车和3辆乙种车载重14吨,5辆甲种车和6辆乙种车载重32吨列方程组求解即可;
(2)先辆甲货车和7辆乙货车一次运送货物的重量,然后再依据总费用=50×总重量求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:
 并在数轴上表示出它的解集.
并在数轴上表示出它的解集.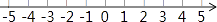
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b,当x=2时y的值是﹣1,当x=﹣1时y的值是5.
(1)求此一次函数的解析式;
(2)若点P(m,n)是此函数图象上的一点,﹣3≤m≤2,求n的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求完成下列题目.
(1)求: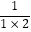 +
+ 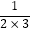 +
+ 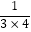 +…+
+…+ 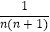 的值. 对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成
的值. 对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成 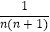 的形式,而
的形式,而 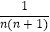 =
= 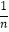 ﹣
﹣ 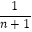 ,这样就把
,这样就把 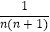 一项(分)裂成了两项.
一项(分)裂成了两项.
试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出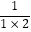 +
+ 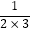 +
+ 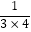 +…+
+…+ 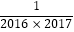 的值.
的值.
(2)若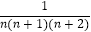 =
= 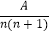 +
+ 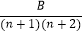 ①求:A、B的值:
①求:A、B的值:
②求: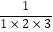 +
+ 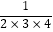 +…+
+…+ 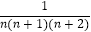 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.必然事件发生的概率为0
B.一组数据1,6,3,9,8的极差为7
C.“面积相等的两个三角形全等”这一事件是必然事件
D.“任意一个三角形的外角和等于180°”这一事件是不可能事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:①AD=DC;②AB=BD;③AB=
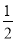 BC;④BD=CD,
BC;④BD=CD,其中正确的个数为( )
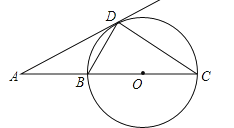
A.4个 B.3个 C.2个 D.1个
相关试题

