【题目】如图,等腰 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 于点
于点 ![]() ,点
,点 ![]() 是
是 ![]() 延长线上一点,点
延长线上一点,点 ![]() 是线段
是线段 ![]() 上一点,
上一点, ![]() ,
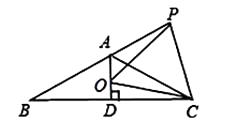
,
下面结论:
① ![]() ;
;
② ![]() 是等边三角形;
是等边三角形;
③ ![]() ;
;
④ ![]() .
.
其中正确的是( ).
A.②③
B.①②④
C.③④
D.①②③④
参考答案:
【答案】D
【解析】连接OB,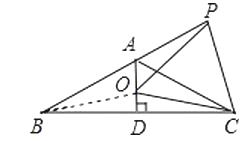
∵AB=AC,AD⊥BC,∴OB=OC, BD=CD,∠BAD= ![]() ∠BAC=
∠BAC= ![]() ×120°=60°,∴∠ABC=90°-∠BAD=30°,
×120°=60°,∴∠ABC=90°-∠BAD=30°,
∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;故①正确;
∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,
∴∠POC=180°-(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC是等边三角形;故②正确;在AC上截取AE=PA,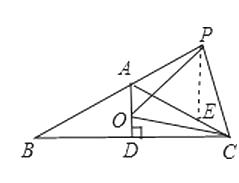
∵∠PAE=180°-∠BAC=60°,∴△APE是等边三角形,∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,∵OP=CP,
在△OPA和△CPE中, 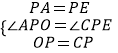 ,∴△OPA≌△CPE(SAS),∴AO=CE,∴AC=AE+CE=AO+AP;故③正确;
,∴△OPA≌△CPE(SAS),∴AO=CE,∴AC=AE+CE=AO+AP;故③正确;
过点C作CH⊥AB于H,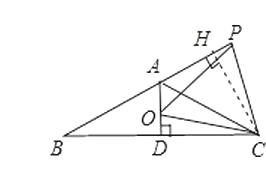
∵∠PAC=∠DAC=60°,AD⊥BC,∴CH=CD,
∴S△ABC= ![]() AB·CH,S四边形AOCP=S△ACP+S△AOC=
AB·CH,S四边形AOCP=S△ACP+S△AOC= ![]() AP·CH+
AP·CH+ ![]() OA·CD
OA·CD
= ![]() AP·CH+
AP·CH+ ![]() OA·CH=
OA·CH= ![]() CH·(AP+OA)=
CH·(AP+OA)= ![]() CH=·AC,
CH=·AC,
∴S△ABC=S四边形AOCP;
故④正确.所以①②③④都正确,故答案为:D.
连接OB,可证明①②正确,在AC上截取AE=PA,可证③正确,过点C作CH⊥AB于H,可证④正确。
-
科目: 来源: 题型:
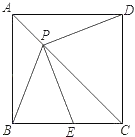
查看答案和解析>>【题目】如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.
(1)求证:①PE=PD;②PE⊥PD;
(2)设AP=x,△PBE的面积为y.
①求出y关于x的函数关系式,并写出x的取值范围;
②当x取何值时,y取得最大值,并求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组数:1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…其中每个数n都连续出现n次,那么这一组数的第119个数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3x=12,3y=4,则3x﹣y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)作△ABC的外接圆;
(2)若AC=BC,AB=8,C到AB的距离是2,求△ABC的外接圆半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的各个内角与它的某个外角的和是2036,求:这个多边形的边数和这个外角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200-2x
已知该商品的进价为每件30元,设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果。
相关试题

