【题目】如图,AB是⊙O的直径,C是⊙O上的一点,过点A作AD⊥CD于点D,交⊙O于点E,且![]() =
=![]() .
.
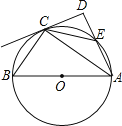
(1)求证:CD是⊙O的切线;
(2)若tan∠CAB=![]() ,BC=3,求DE的长.
,BC=3,求DE的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,由![]() =
=![]() ,根据圆周角定理得∠1=∠2,而∠1=∠OCA,则∠2=∠OCA,则可判断OC∥AD,由于AD⊥CD,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠1=∠2,而∠1=∠OCA,则∠2=∠OCA,则可判断OC∥AD,由于AD⊥CD,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连接BE交OC于F,由AB是⊙O的直径得∠ACB=90°,在Rt△ACB中,根据正切的定义得AC=4,再利用勾股定理计算出AB=5,然后证明Rt△ABC∽Rt△ACD,利用相似比先计算出AD=![]() ,再计算出CD=
,再计算出CD=![]() ;根据垂径定理的推论由
;根据垂径定理的推论由![]() =
=![]() 得OC⊥BE,BF=EF,于是可判断四边形DEFC为矩形,所以EF=CD=
得OC⊥BE,BF=EF,于是可判断四边形DEFC为矩形,所以EF=CD=![]() ,则BE=2EF=
,则BE=2EF=![]() ,然后在Rt△ABE中,利用勾股定理计算出AE=
,然后在Rt△ABE中,利用勾股定理计算出AE=![]() ,再利用DE=AD﹣AE求解.
,再利用DE=AD﹣AE求解.
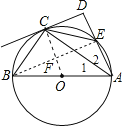
(1)证明:连接OC,如图,
∵![]() =
=![]() ,
,
∴∠1=∠2,
∵OC=OA,
∴∠1=∠OCA,
∴∠2=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连接BE交OC于F,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,tan∠CAB=![]() =
=![]() ,
,
而BC=3,
∴AC=4,
∴AB=![]() =5,
=5,
∵∠1=∠2,
∴Rt△ABC∽Rt△ACD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得AD=
,解得AD=![]() ,
,
∵![]() =
=![]() ,即
,即![]() =
=![]() ,解得CD=
,解得CD=![]() ,
,
∵![]() =
=![]() ,
,
∴OC⊥BE,BF=EF,
∴四边形DEFC为矩形,
∴EF=CD=![]() ,
,
∴BE=2EF=![]() ,
,
∵AB为直径,
∴∠BEA=90°,
在Rt△ABE中,
AE=![]() =
=![]() =
=![]() ,
,
∴DE=AD﹣AE=![]() ﹣
﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段不可能组成三角形的是( )
A. 1、2、3 B. 2、3、4 C. 3、4、5 D. 4、5、6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )

A.
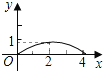 B.
B.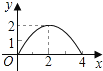
C.
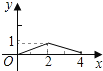 D.
D.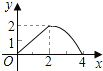
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
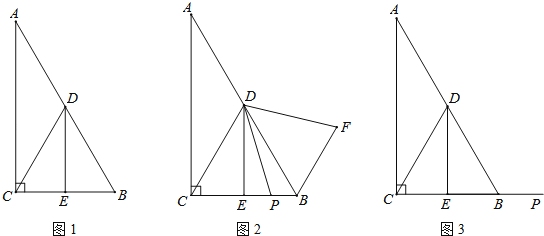
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=
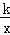 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).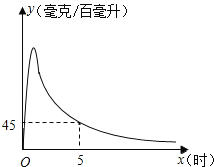
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式mx2﹣m与多项式x2﹣2x+1的公因式是( ).
A.x﹣1 B.x+1 C.x2﹣1 D.(x﹣1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式中成立的是( )
A. a4a=a4 B. a6﹣a3=a3 C. (ab2)3=a3b5 D. (a3)2=a6
相关试题

