【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
![]()
参考答案:
【答案】(1)3;5;1或5;(2)6(3)9
【解析】
试题(1)根据数轴,观察两点之间的距离即可解决;
(2)根据|a+4|+|a-2|表示数a的点到-4与2两点的距离的和即可求解.
试题解析:(1)3;5;1或5;
(2)∵![]() 表示数轴上数
表示数轴上数![]() 和数-4,2之间距离的和,又因为
和数-4,2之间距离的和,又因为![]() 位于-4,2之间,
位于-4,2之间,
∴![]() 等于-4,2之间的距离和,
等于-4,2之间的距离和,
即![]() =|2-(-4)|=6.
=|2-(-4)|=6.
(3)∵![]() 表示数轴上数
表示数轴上数![]() 和数-5,1,4之间距离的和,
和数-5,1,4之间距离的和,
∴a=1时距离的和最小
∴![]() =
=![]() =|4-(-5)|=9
=|4-(-5)|=9
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习代数式的值时,介绍了计算程序中的框图:用“
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条).按图所示的程序计算(输入的
”表示数据判断框(根据条件决定执行两条路径中的某一条).按图所示的程序计算(输入的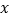 为正整数).
为正整数).例如:输入
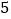 ,结果依次为
,结果依次为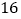 、
、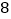 、
、 、
、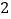 、
、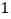 ,即运算循环
,即运算循环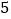 次(第
次(第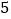 次计算结果为
次计算结果为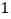 )结束.
)结束.(1)输入
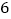 ,结果依次为
,结果依次为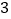 、___________________、
、___________________、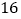 、
、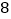 、
、 、
、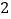 、
、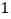 .
.(依次填入循环计算所缺的几次结果)
(2)输入
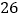 ,运算循环__________次结束.
,运算循环__________次结束.(3)输入正整数
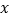 ,经过
,经过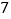 次运算结束,试求
次运算结束,试求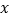 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角.
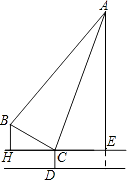
(1)求证:AB=AC
(2)求吊车的吊臂顶端A点距地面的高度是多少米?(保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.

(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△PAC为等边三角形,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】课外兴趣小组活动时,老师出示了如下问题:如图①,已知在四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=
 AC.
AC.小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决该问题.
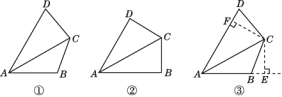
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图②,可证AB+AD=
 AC.请你完成此证明.
AC.请你完成此证明.(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB,AD的垂线,垂足分别为点E,F,如图③.请你补全证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.

(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点P1(﹣1,m),P2(﹣2,n)在反比例函数y=
 (k>0)的图像上,则mn(填“>”“<”或“=”号).
(k>0)的图像上,则mn(填“>”“<”或“=”号).
相关试题

