【题目】如图1,等腰Rt△ABC和等腰Rt△DEF中,∠BCA=∠FDE=90°,AB=4![]() ,EF=8
,EF=8![]() .点A、C、D、E在一条直线上,等腰Rt△DEF静止不动,初始时刻,C与D重合,之后等腰Rt△ABC从C出发,沿射线CE方向以每秒1个单位长度的速度匀速运动,当A点与E点重合时,停止运动.设运动时间为t秒(t≥0).
.点A、C、D、E在一条直线上,等腰Rt△DEF静止不动,初始时刻,C与D重合,之后等腰Rt△ABC从C出发,沿射线CE方向以每秒1个单位长度的速度匀速运动,当A点与E点重合时,停止运动.设运动时间为t秒(t≥0).
(1)直接写出线段AC、DE的长度;
(2)在等腰Rt△ABC的运动过程中,设等腰Rt△ABC和等腰Rt△DEF重叠部分的面积为S,请直接写出S与t的函数关系式和相应的自变量t的取值范围;
(3)在整个运动过程中,当线段AB与线段EF相交时,设交点为点M,点O为线段CE的中点;是否存在这样的t,使点E、O、M三点构成的三角形是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.

参考答案:
【答案】(1)AC=4,DE=8,;(2)见解析;(3)见解析.
【解析】
(1)利用运动即可得出结论;
(2)利用面积的和差和特殊图形的面积公式分三种情况讨论计算即可;
(3)找出△MOE是等腰三角形时的位置即可得出结论.
(1)在Rt△ABC中,

AC=BC,AB=4![]() ,
,
∴AC=BC=4,
同理:DE=DF=8;
(2)当0<t≤4时,如图1,设AB与BD的交点为G,
由运动知,CD=t,
∴DG=AD=4﹣t,
∴S=![]() (DG+BC)×CD=
(DG+BC)×CD=![]() (4﹣t+4)×t=﹣
(4﹣t+4)×t=﹣![]() t2+4t,
t2+4t,
当4<t≤8时,

如图3,记AB与EF的交点为P,
由运动知,CE=8﹣t,
∴CQ=8﹣t,
∴BQ=4﹣(8﹣t)=t﹣4,
∴S=S△ABC﹣S△PBQ=![]() ×4×4﹣
×4×4﹣![]() (t﹣4)×
(t﹣4)×![]() (t﹣4)=8﹣
(t﹣4)=8﹣![]() (t﹣4)2,
(t﹣4)2,
当8<t<12时,如图5,

记AB与EF的交点为N',
由运动知,AC=4﹣(t﹣8)=t﹣4,
∴S=S△AEN'=![]() (t﹣4)×
(t﹣4)×![]() (t﹣4)=
(t﹣4)=![]() (t﹣4)2;
(t﹣4)2;
(3)当∠MOE=90°时,如图6,

即:点C与O重合,
∴t=4,
当∠OME=90°时,如图7,

点A和O重合,
∴t=8,
即:△MOE是等腰三角形时,t=4或8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
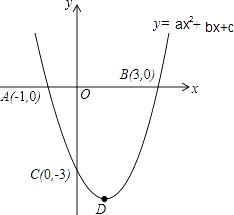
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,我们在“格点”直角坐标系上可以看到,要求AB或CD的长度,可以转化为求Rt△ABC或Rt△DEF的斜边长.
例如:从坐标系中发现:D(﹣7,3),E(4,﹣3),所以DF=|5﹣(﹣3)|=8,EF=|4﹣(﹣7)|=11,所以由勾股定理可得:DE=
 .
.(1)在图①中请用上面的方法求线段AB的长:AB= ;
(2)在图②中:设A(x1,y1),B(x2,y2),试用x1,x2,y1,y2表示:AC= ,BC= ,AB= ;
(3)试用(2)中得出的结论解决如下题目:已知:A(2,1),B(4,3);
①直线AB与x轴交于点D,求线段BD的长;
②C为坐标轴上的点,且使得△ABC是以AB为边的等腰三角形,请求出C点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
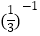 +|1﹣
+|1﹣ 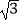 |﹣2sin60°+(π﹣2016)0﹣
|﹣2sin60°+(π﹣2016)0﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
-
科目: 来源: 题型:
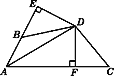
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
相关试题

