【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(0,–3),(2,–3).
经过点(0,–3),(2,–3).
(1)求抛物线的表达式;
(2)求抛物线的顶点坐标及与x轴交点的坐标;
参考答案:
【答案】(1)抛物线的表达式为:![]() ;
;
(2)抛物线与x轴交点的坐标为(–1,0),(3,0).
【解析】分析:(1)把两个已知点的坐标代入得到关于b、c的方程组,然后解方程组即可确定抛物线解析式; (2)把(1)中的一般式配成顶点式即可得到抛物线的顶点坐标,然后通过解可得到抛物线与x轴的交点坐标.
本题解析:(1)把(0,–3)代入![]() , ∴
, ∴![]() ,
,
把(2,–3)代入![]() , ∴
, ∴![]() ,
,
所以抛物线解析式为: ![]() .
.
(2)由(1)得![]() . ∴顶点坐标为(1,–4),
. ∴顶点坐标为(1,–4),
由![]() 解得
解得![]() .
.
∴抛物线与x轴交点的坐标为(–1,0),(3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,E为BC延长线上一点,∠A=50°,则∠DCE的度数为( )
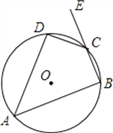
A. 40° B. 50° C. 60° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题提出】
平面上,若点P与A、B、C三点中的任意两点均构成等腰三角形,则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形,也称点P是△ABC的巧妙点.
【初步思考】
(1)如图①,在等边△ABC的内部和外部各作一个△ABC的巧妙点.(尺规作图,不写作法,保留作图痕迹)
(2)如图②,在△ABC中,AB=AC,∠BAC=36°,点D、E是△ABC的两个巧妙点,其中AD=AB,AE=AC,BD=BC=CE,连接DE,分别交AB、AC于点M、N.求证: DA2=DB·DE.

【深入研究】
(3)在△ABC中,AB=AC,若存在一点P,使PB=BA,PA=PC.点P可能为△ABC的巧妙点吗?若可能,请画出示意图,并直接写出∠BAC的度数;若不可能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子里装有4个小球,分别标有1,2,3,7四个数字,这些小球除所标数字不同外,其余方面完全相同,甲、乙两人每次同时从袋子中各随机摸出一个小球,记下小球上的数字,并计算它们的和.
(1)请用画树状图或列表的方法,求两数和是8的概率;
(2)甲、乙两人想用这种方法做游戏,他们规定:若两数之和是2的倍数时,甲得3分;若两数之和是3的倍数时,乙得2分;当两数之和是其他数值时,两人均不得分.你认为这个游戏公平吗?请说明理由;若你认为不公平,请你修改得分规则,使游戏公平。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店卖苹果,第一天卖出m千克,第二天比第一天多卖出2千克,第三天卖出的是第一天的3倍,求这个水果店三天一共卖出苹果多少千克?(用含m的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】设S=(1+2)(1+22)(1+24)(1+28)(1+216),则S+1=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留在一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示x与y之间的关系,
请根据图象解决下列问题:
(1)甲乙两地之间的距离为_____千米;
(2)求快车和慢车的速度;
(3)点D表示_____点E表示_____.

相关试题

