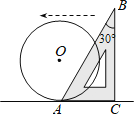
【题目】如图,半径为4的![]() 与含有
与含有![]() 角的真角三角板ABC的边AC切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与
角的真角三角板ABC的边AC切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与![]() 相切时,该直角三角板平移的距离为
相切时,该直角三角板平移的距离为![]()
![]()
A. 2 B. ![]() C. 4 D.
C. 4 D. ![]()
参考答案:
【答案】D
【解析】
根据题意画出平移后的图形,如图所示,设平移后的![]() 与圆O相切于点D,连接OD,OA,AD,过O作
与圆O相切于点D,连接OD,OA,AD,过O作![]() ,根据垂径定理得到E为AD的中点,由平移前AC与圆O相切,切点为A点,根据切线的性质得到OA与AC垂直,可得
,根据垂径定理得到E为AD的中点,由平移前AC与圆O相切,切点为A点,根据切线的性质得到OA与AC垂直,可得![]() 为直角,由
为直角,由![]() 与
与![]() 为圆O的两条切线,根据切线长定理得到
为圆O的两条切线,根据切线长定理得到![]() ,再根据
,再根据![]() ,根据有一个角为
,根据有一个角为![]() 的等腰三角形为等边三角形可得出三角形
的等腰三角形为等边三角形可得出三角形![]() 为等边三角形,平移的距离
为等边三角形,平移的距离![]() ,且
,且![]() ,由
,由![]() 求出
求出![]() 为
为![]() ,在直角三角形AOE中,由锐角三角函数定义求出AE的长,由
,在直角三角形AOE中,由锐角三角函数定义求出AE的长,由![]() 可求出AD的长,即为平移的距离.
可求出AD的长,即为平移的距离.
解:根据题意画出平移后的图形,如图所示:
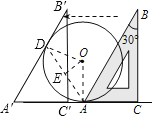
设平移后的![]() 与圆O相切于点D,连接OD,OA,AD,
与圆O相切于点D,连接OD,OA,AD,
过O作![]() ,可得E为AD的中点,
,可得E为AD的中点,
![]() 平移前圆O与AC相切于A点,
平移前圆O与AC相切于A点,
![]() ,即
,即![]() ,
,
![]() 平移前圆O与AC相切于A点,平移后圆O与
平移前圆O与AC相切于A点,平移后圆O与![]() 相切于D点,
相切于D点,
即![]() 与
与![]() 为圆O的两条切线,
为圆O的两条切线,
![]() ,又
,又![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
则该直角三角板平移的距离为![]() .
.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交于点
与x轴交于点 ,与BC交于点C,连接AC、BC,已知
,与BC交于点C,连接AC、BC,已知 .
.


 求点B的坐标及抛物线的解析式;
求点B的坐标及抛物线的解析式; 点P是线段BC上的动点
点P是线段BC上的动点 点P不与B、C重合
点P不与B、C重合 ,连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
,连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x. 记
记 的面积为S,求S关于x的函数表达式并求出当
的面积为S,求S关于x的函数表达式并求出当 时x的值;
时x的值; 记点P的运动过程中,
记点P的运动过程中,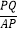 是否存在最大值?若存在,求出
是否存在最大值?若存在,求出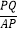 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 中,点
中,点 在
在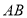 边上,
边上, 交边
交边 于点
于点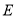 ,且
,且 平分
平分 .
.(1)求证:
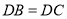 ;
;(2)如图2,在
 边上取点
边上取点 ,使
,使 ,若
,若 ,
,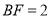 ,求
,求 的长。
的长。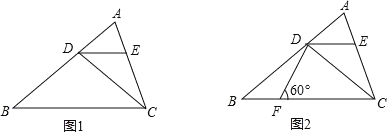
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边
是等边 的外角
的外角 内部的一条射线,点
内部的一条射线,点 关于
关于 的对称点为
的对称点为 ,连接
,连接 ,
, ,
,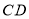 ,其中
,其中 、
、 分别交射线
分别交射线 于点
于点 ,
, .
.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)若
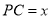 ,
,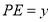 ,求
,求 的长度(用
的长度(用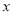 ,
, 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝是广西盛产的一种水果,六月份是荔技传统销售旺季
 去年六月份某水果公司为拓展销售渠道,在实体店的基础上中途增设了网店,公司总销售量
去年六月份某水果公司为拓展销售渠道,在实体店的基础上中途增设了网店,公司总销售量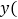 吨
吨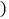 与销售时间
与销售时间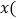 天
天 关系如图所示:
关系如图所示: 请直接写出去年六月份网店每天的销售量,并求出AB的解析式
请直接写出去年六月份网店每天的销售量,并求出AB的解析式 不写取值范围
不写取值范围 ;
; 公司预计,今年六月份实体店的销售量与去年相同,网店的销售量将有所增加,预计今年网店每天的销售量比去年增加
公司预计,今年六月份实体店的销售量与去年相同,网店的销售量将有所增加,预计今年网店每天的销售量比去年增加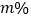 ,公司六月份的总销售量是去年的
,公司六月份的总销售量是去年的 倍,求m的值.
倍,求m的值.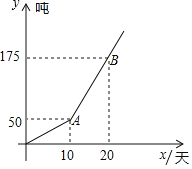
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)
 (2)
(2) -
- -2
-2
(3)
 (代入法) (4)
(代入法) (4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
(1)B出发时与A相距 千米。
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时。
(3)B出发后 小时与A相遇。
(4)求出A行走的路程S与时间t的函数关系式。
(5)求出当 t≥1.5时B走的路程S与时间t的函数关系式

相关试题

