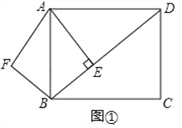
【题目】已知:如图①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,平移中的△ABF为△A1B1F1设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).
①当点F分别平移到线段AB上时,求出m的值
②当点F分别平移到线段AD上时,当直接写出相应的m的值.
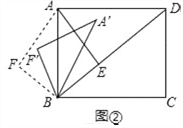
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AE交于点O,当∠A′BD=∠FAB时,请直接写出OB的长.
参考答案:
【答案】(1)AE=4,BE=3;(2)①3;②![]() ;(3)1或
;(3)1或![]() .
.
【解析】分析:(1)利用矩形性质、勾股定理及三角形面积公式求解;(2)依题意画出图形,如答图2所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;(3)在旋转过程中,分两种情形分别求解即可.
本题解析:
(1)在Rt△ABD中,AB=5,AD=![]() ,
,
由勾股定理得:BD=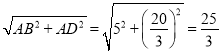 .
.
∵S△ABD=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE=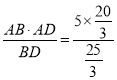 =4.
=4.
在Rt△ABE中,AB=5,AE=4,由勾股定理得:BE=3.
(2)设平移中的三角形为△A′B′F′,如答图2所示:
由对称点性质可知,∠1=∠2.
由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′=3.
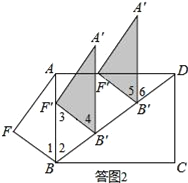
①当点F′落在AB上时,
∵AB∥A′B′,∴∠3=∠4,∴∠3=∠2,
∴BB′=B′F′=3,即m=3;
②当点F′落在AD上时,
∵AB∥A′B′,∴∠6=∠2,
∵∠1=∠2,∠5=∠1,∴∠5=∠6,
又易知A′B′⊥AD,
∴△B′F′D为等腰三角形,∴B′D=B′F′=3,
∴BB′=BD﹣B′D=![]() ﹣3=
﹣3=![]() ,即m=
,即m=![]() .
.
(3)如图3中,设AE交BA′于K.
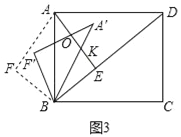
∵∠KBE=∠FAB=∠BAE,∠KEB=∠AEB,
∴△EKB∽△EBA,∴可得BE2=EKEA,∴EK=![]() ,
,
在Rt△BEK中,BK=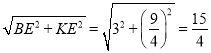 ,
,
∴A′K=5﹣![]() =
=![]() ,∵∠A′=∠KBE,∴OA′∥BE,∴
,∵∠A′=∠KBE,∴OA′∥BE,∴![]() ,
,
∴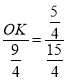 ,∴OK=
,∴OK=![]() ,∴AO=AE﹣OK=KE=1.
,∴AO=AE﹣OK=KE=1.
如图4中,当∠DBA′=∠BAF时,点A′在线段BC上,
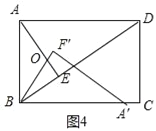
易证∠OAB=∠OBA,∴OA=OB,设OA=OB=x,
在Rt△OBE中,∵OB2=OE2+BE2,∴x2=32+(4﹣x)2,
∴x=![]() ,∴OA=
,∴OA=![]() ,
,
综上所述,满足条件的OA的长为1或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件属于随机事件的是( )
A.明天的早晨,太阳从东方升起B.13人中至少有两人同生肖
C.抛出一枚骰子,点数为0D.打开电视机,正在播放广告
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(m,n)在第二象限,那么点B(﹣m,|n|)在( )
A.第一象限
B.第二象限;
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:[(3x+2y)(3x﹣2y)﹣(x+2y)(3x﹣2y)]÷x,其中x=2,y=﹣1.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了备战2016年里约奥运会,中国射击队正在积极训练.甲、乙两名运动员在相同的条件下,各射击10次.经过计算,甲、乙两人成绩的平均数均是9.5环,甲的成绩方差是0.125,乙的成绩的方差是0.85,那么这10次射击中,甲、乙成绩的稳定情况是( )
A.甲较为稳定
B.乙较为稳定
C.两个人成绩一样稳定
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校1000名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
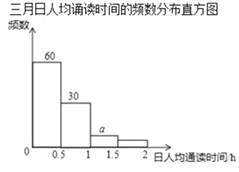
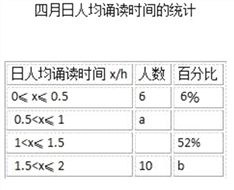
根据以上信息,解答下列问题:
(1)本次调查的学生数为 人;
(2)四月日均诵读时间的统计表中的a值分别为 ;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多 人;
(4)根据抽样调查结果,请你估计该校学生四月份人均诵读时间在1小时以上的人数.
-
科目: 来源: 题型:
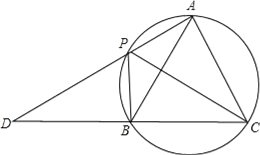
查看答案和解析>>【题目】如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2

①求PD的长.
②图中弧BP和线段DP、BD组成的图形面积为 (结果保留π)
相关试题

