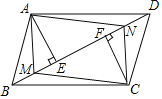
【题目】如图,BD是ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E,F,AM与CN分别是∠BAE与∠DCF的平分线,AM交BE于点M,CN交DF于点N,连接AN,CM.求证:四边形AMCN是平行四边形.
参考答案:
【答案】见解析.
【解析】
连接AC交BD于O,由平行四边形的性质得出OA=OC,OB=OD,AB=CD,AB∥CD,由ASA证明△ABM≌△CDN,得出BM=DN,证出OM=ON,即可得出结论.
证明:连接AC交BD于O,如图所示:
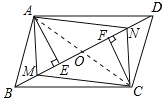
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB=CD,AB∥CD,
∴∠ABM=∠CDN,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∴∠ABM+∠BAE=90°,∠CDN+∠DCF=90°,
∴∠BAE=∠DCF,
∵AM与CN分别是∠BAE与∠DCF的平分线,
∴∠BAM=∠DCN,
在△ABM和△CDN中,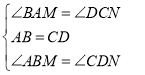 ,
,
∴△ABM≌△CDN(ASA),
∴BM=DN,
∴OM=ON,
又∵OA=OC,
∴四边形AMCN是平行四边形.
-
科目: 来源: 题型:
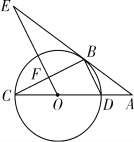
查看答案和解析>>【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
-
科目: 来源: 题型:
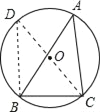
查看答案和解析>>【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=
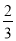 ,求BC的长.
,求BC的长.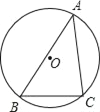
【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵
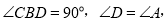
∴
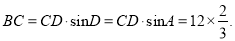
∴
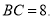
点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22【题目】如图,一次函数y=k1x+b与反比例函数y=
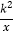 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>
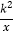 的解集;
的解集;(3)若P(p,y1),Q(﹣2,y2)是函数y=
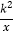 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.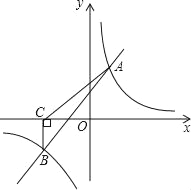
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市在“十一”长假期间对顾客实行优惠,规定如下:
一次性购物金额
优惠办法
不超过100元
不予优惠
超过100元但不超过500元
超过100元部分给予九折优惠
超过500元
超过500元部分给予八折优惠
(1)小明的爷爷一次性购200元的保健食品,他实际付款_____元;小明妈妈一次性购300元的衣服,她实际付款_____元;如果他们两人合作付款,则能少付_____元;
(2)小芳奶奶在该超市一次性购物x元生活用品,当x大于或等于500时,她实际付款_____元;(用含x的式子表示,写最简结果)
(3)如果小芳奶奶两次购物货款合计900元,第一次购物的货款为a元(
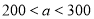 ),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)
),两次购物小芳奶奶实际付款多少元?(用含a的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
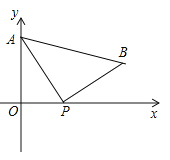
(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
-
科目: 来源: 题型:
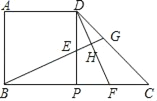
查看答案和解析>>【题目】已知,正方形ABPD的边长为3,将边DP绕点P顺时针旋转90°至PC,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF,连接BE并延长分别交DF、DC于H、G.
(1)①求证:△BPE≌△DPF,②判断BG与DF位置关系并说明理由;
(2)当PE的长度为多少时,四边形DEFG为菱形并说明理由;
(3)连接AH,在点E、F运动的过程中,∠AHB的大小是否发生改变?若改变,请说出是如何变化的;若不改变,请求出∠AHB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个三角形,分别连接这个三角形三边的中点得到图b;再分别连接图b中间小三角形的三边的中点,得到图c
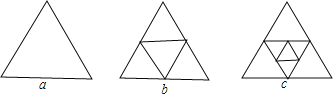
(1)图b有 个三角形,图c有 个三角形.
(2)按上面的方法继续下去,第n个图形中有多少个三角形(用n的代数式表示结论).
(3)当n=10时,第10个图形中有多少个三角形?
相关试题

