【题目】甲、乙两人从少年宫出发,沿相同的路分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.
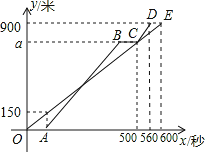
(1)在跑步的全过程中,甲共跑了 米, 甲的速度为 米/秒;
(2)乙跑步的速度是多少?乙在途中等候甲用了多长时间?
(3)甲出发多长时间第一次与乙相遇?此时乙跑了多少米?
参考答案:
【答案】(1)900,1.5米/秒;(2)100秒.(3)甲出发250秒和乙第一次相遇,此时乙跑了375米.
【解析】
试题分析:(1)终点E的纵坐标就是路程,横坐标就是时间;
(2)首先求得C点对用的横坐标,即a的值,则CD段的路程可以求得,时间是560-500=60秒,则乙跑步的速度即可求得;
B点时,所用的时间可以求得,然后求得路程是150米时,甲用的时间,就是乙出发的时刻,两者的差就是所求;
(3)首先求得甲运动的函数以及AB段的函数,求出两个函数的交点坐标即可.
试题解析:(1)根据图象可以得到:甲共跑了900米,用了600秒,则速度是:900÷600=1.5米/秒;
(2)甲跑500秒时的路程是:500×1.5=750米,则CD段的长是900-750=150米,时间是:560-500=60秒,则速度是:150÷60=2.5米/秒;
甲跑150米用的时间是:150÷1.5=100秒,则甲比乙早出发100秒.
乙跑750米用的时间是:750÷2.5=300秒,则乙在途中等候甲用的时间是:500-300-100=100秒.
(3)甲每秒跑1.5米,则甲的路程与时间的函数关系式是:y=1.5x,
乙晚跑100秒,且每秒跑2.5米,则AB段的函数解析式是:y=2.5(x-100),
根据题意得:1.5x=2.5(x-100),解得:x=250秒.
乙的路程是:2.5×(250-100)=375(米).
答:甲出发250秒和乙第一次相遇,此时乙跑了375米.
-
科目: 来源: 题型:
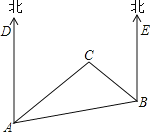
查看答案和解析>>【题目】如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西50°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O,BE=CD。
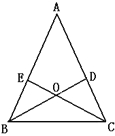
(1)△ABC是等腰三角形吗?为什么?
(2)点O在∠A的平分线上吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】规律探究.下面有8个算式,排成4行2列
2+2, 2×2
3+
 , 3×
, 3×
4+
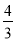 , 4×
, 4×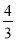
5+
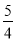 , 5×
, 5×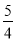 ……, ……
……, ……(1)同一行中两个算式的结果怎样?
(2)算式2005+
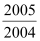 和2005×
和2005×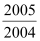 的结果相等吗?
的结果相等吗?(3)请你试写出算式,试一试,再探索其规律,并用含自然数n的代数式表示这一规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是立方体和长方体模型,立方体棱长和长方体底面各边长都为1,长方体侧棱长为2,现用60张长为6,宽为4的长方形卡纸,剪出这两种模型的表面展开图,有两种方法:
方法一:如图2,每张卡纸剪出3个立方体表面展开图;
方法二:如图3,每张卡纸剪出2个长方体表面展开图(图中只画出1个).

设用x张卡纸做立方体,其余卡纸做长方体,共做两种模型y个.要求制作的长方体的个数不超过立方体的个数.
(1)在图3中画出第二个长方体表面展开图,用阴影表示;
(2)请你写出y关于x的函数解析式,并注明自变量x的取值范围;
(3)设每只模型(包括立方体和长方体)平均获利为w(元),w满足函数
 ,
,若想将模型作为教具卖出获得最大利润,则应该制作立方体和长方体各多少个?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)若降价的最小单位为1元,则当降价多少元时,每星期的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
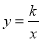 与
与 (
(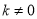 )在同一直角坐标系中的大致图象可能是( )
)在同一直角坐标系中的大致图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

