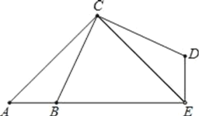
【题目】如图,已知△ACE是等腰直角三角形,∠ACE=90°,B点为AE上一点,△CAB经过逆时针旋转后到达△CED的位置.
问:(1)旋转中心是哪个点?旋转角是哪个角?旋转了多少度?
(2)图中哪两个三角形全等?
(3)若∠ACB=20°.则∠CDE= ,∠DEB= .
参考答案:
【答案】(1)C点;∠ACE或∠BCD;90度;(2)△CAB和△CED全等;(3)115°,90°.
【解析】
(1)利用旋转的定义求解;
(2)根据旋转的性质进行判断;
(3)先利用等腰直角三角形的性质得∠A=∠CEA=45°,则根据三角形内角和可计算出∠ABC=115°,再根据旋转的性质得∠CDE=∠ABC=115°,∠CED=∠A=45°,从而得到∠DEB=90°.
(1)旋转中心是C点;旋转角为∠ACE或∠BCD;旋转了90度;
(2)图中△CAB和△CED全等;
(3)∵△ACE是等腰直角三角形,∠ACE=90°,
∴∠A=∠CEA=45°.
∵∠ACB=20°,
∴∠ABC=180°﹣45°﹣20°=115°.
∵△CAB经过逆时针旋转后到达△CED的位置,
∴∠CDE=∠ABC=115°,∠CED=∠A=45°,
∴∠DEB=45°+45°=90°.
故答案为:115°,90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=2cm,AE=1cm,求⊙O的半径.
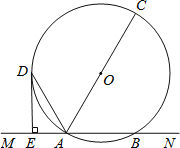
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在Rt△ABC 中,
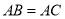 ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△ 绕点
绕点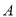 逆时针旋转90后,得到△
逆时针旋转90后,得到△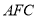 ,连接
,连接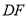 .
.(1)试说明:△
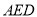 ≌△
≌△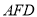 ;
; (2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
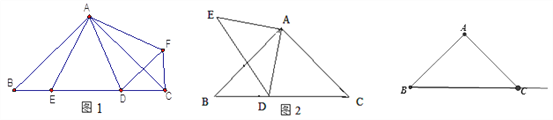
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
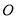 是坐标原点,正方形
是坐标原点,正方形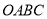 的顶点
的顶点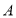 、
、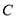 分别在
分别在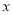 轴与
轴与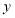 轴上,已知正方形边长为3,点
轴上,已知正方形边长为3,点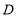 为
为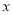 轴上一点,其坐标为
轴上一点,其坐标为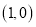 ,连接
,连接 ,点
,点 从点
从点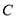 出发以每秒1个单位的速度沿折线
出发以每秒1个单位的速度沿折线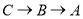 的方向向终点
的方向向终点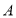 运动,当点
运动,当点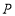 与点
与点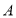 重合时停止运动,运动时间为
重合时停止运动,运动时间为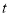 秒.
秒.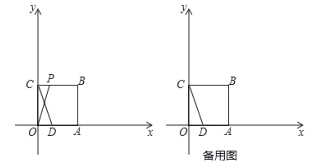
(1)连接
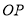 ,当点
,当点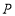 在线段
在线段 上运动,且满足
上运动,且满足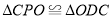 时,求直线
时,求直线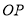 的表达式;
的表达式;(2)连接
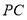 、
、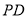 ,求
,求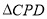 的面积
的面积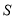 关于
关于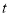 的函数表达式;
的函数表达式;(3)点
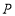 在运动过程中,是否存在某个位置使得
在运动过程中,是否存在某个位置使得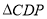 为等腰三角形,若存在,直接写出点
为等腰三角形,若存在,直接写出点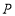 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
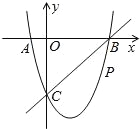
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,﹣4)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:① abc>0;② 2a+b=0;③ 当m≠1时,a+b>am2+bm;④ a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2,
其中正确的有( )

A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
相关试题

