【题目】如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
参考答案:
【答案】
(1)证明:由题意得:AE=2t,CD=4t,

∵DF⊥BC,
∴∠CFD=90°,
∵∠C=30°,
∴DF= ![]() CD=
CD= ![]() ×4t=2t,
×4t=2t,
∴AE=DF;
∵DF⊥BC,
∴∠CFD=∠B=90°,
∴DF∥AE,
∴四边形AEFD是平行四边形
(2)证明:四边形AEFD能够成为菱形,理由是:

由(1)得:AE=DF,
∵∠DFC=∠B=90°,
∴AE∥DF,
∴四边形AEFD为平行四边形,
若AEFD为菱形,则AE=AD,
∵AC=100,CD=4t,
∴AD=100﹣4t,
∴2t=100﹣4t,
t= ![]() ,
,
∴当t= ![]() 时,四边形AEFD能够成为菱形;
时,四边形AEFD能够成为菱形;
(3)证明:分三种情况:
①当∠EDF=90°时,如图3,

则四边形DFBE为矩形,
∴DF=BE=2t,
∵AB= ![]() AC=50,AE=2t,
AC=50,AE=2t,
∴2t=50﹣2t,
t= ![]() ,
,
②当∠DEF=90°时,如图4,

∵四边形AEFD为平行四边形,
∴EF∥AD,
∴∠ADE=∠DEF=90°,
在Rt△ADE中,∠A=60°,AE=2t,
∴AD=t,
∴AC=AD+CD,
则100=t+4t,
t=20,
③当∠DFE=90°不成立;
综上所述:当t为 ![]() 或20时,△DEF为直角三角形
或20时,△DEF为直角三角形
【解析】(1)根据时间和速度表示出AE和CD的长,利用30°所对的直角边等于斜边的一半求出DF的长为4t,则AE=DF,再证明,AE∥DF即可解决问题.(2)根据(1)的结论可以证明四边形AEFD为平行四边形,如果四边形AEFD能够成为菱形,则必有邻边相等,则AE=AD,列方程求出即可;(3)当△DEF为直角三角形时,有三种情况:①当∠EDF=90°时,如图3,②当∠DEF=90°时,如图4,③当∠DFE=90°不成立;分别找一等量关系列方程可以求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正n边形的一个内角为135°,那么n的值为( )
A.12B.10C.8D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
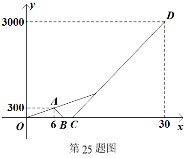
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
⑴小亮在家停留了 分钟.
⑵求小亮骑单车从家出发去图书馆时距家的路程y(米)与出发时间x(分钟)之间的函数关系式.
⑶若小亮和姐姐到图书馆的实际时间为m分钟,原计划步行到达图书馆的时间为n分钟,则n-m= 分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:

(1)填空:甲种收费的函数关系式是 . 乙种收费的函数关系式是 .
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数图象经过不同象限的两点A(m,﹣1),B(﹣5,n),则下列判断正确的是( )
A.m>0,n>0B.m>0,n<0C.m<0,n>0D.m<0,n<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( )
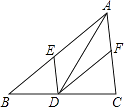
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD⊥BC,那么四边形AEDF是菱形
D.如果AD平分∠BAC,那么四边形AEDF是菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】命题“对角线相等”的逆命题是_____.
相关试题

