搜索
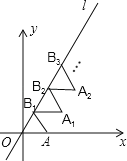
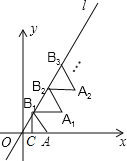
【题目】如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为1的等边三角形，点A在x轴上，点O，B1，B2，B3，…都在直线l上，则点A2016的坐标是______．
参考答案：
【答案】（1009，1008
）
【解析】
根据题意得出直线OB1的解析式为y=x，进而得出O，B1，B2，B3坐标，进而得出坐标变化规律，进而得出答案．
过B1向x轴作垂线B1C，垂足为C，
由题意可得：A（1，0），AO∥A1B1，∠B1OC＝30°，
∴CB1＝OB1cos30°＝
，
∴B1的横坐标为：
，则B1的纵坐标为：，
∴点B1，B2，B3，…都在直线y＝x上，
∴B1（，），
同理可得出：A的横坐标为：1，
∴y＝，
∴A2（2，），
…
An（1+
，
）．
∴A2016（1009，1008），
故答案为：（1009，1008）
-
科目： 来源： 题型：
查看答案和解析>>【题目】“绿水青山就是金山银山”，为保护生态环境，A，B两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：
村庄
清理养鱼网箱人数/人
清理捕鱼网箱人数/人
总支出/元
A
15
9
57000
B
10
16
68000
（1）若两村清理同类渔具的人均支出费用一样，求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元；
（2）在人均支出费用不变的情况下，为节约开支，两村准备抽调40人共同清理养鱼网箱和捕鱼网箱，要使总支出不超过102000元，且清理养鱼网箱人数小于清理捕鱼网箱人数，则有哪几种分配清理人员方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知反比例函数y1=
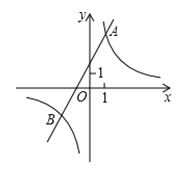
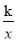的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .(1)求这两个函数的关系式；
(2)观察图象,直接写出使得y1>y2成立的自变量x的取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】【题目】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=一的图象上一部分,请根据图中信息解答下列问题
(1)恒温系统在这天保持大棚内温度20℃的时间有多少小时?
(2)求k的值；
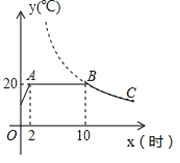
(3)当x=20时,大棚内的温度约为多少度?
-
科目： 来源： 题型：
查看答案和解析>>【题目】某研究所将某种材料加热到1000℃时停止加热，并立即将材料分为A、B两组，采用不同工艺做降温对比实验，设降温开始后经过x min时，A、B两组材料的温度分别为yA℃、yB℃，yA、yB与x的函数关系式分别为yA=kx+b，yB=
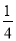（x﹣60）2+m（部分图象如图所示），当x=40时，两组材料的温度相同．
（1）分别求yA、yB关于x的函数关系式；
（2）当A组材料的温度降至120℃时，B组材料的温度是多少？
（3）在0＜x＜40的什么时刻，两组材料温差最大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列方程的特征及其解的特点．
①x＋
＝－3的解为x1＝－1，x2＝－2；②x＋
＝－5的解为x1＝－2，x2＝－3；③x＋
＝－7的解为x1＝－3，x2＝－4.解答下列问题：
(1)请你写出一个符合上述特征的方程为________，其解为________；
(2)根据这类方程的特征，写出第n个方程为________，其解为________；
(3)请利用(2)的结论，求关于x的方程x＋
＝－2(n＋2)(其中n为正整数)的解． -
科目： 来源： 题型：
查看答案和解析>>【题目】某商店准备购进
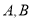两种商品，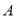
种商品毎件的进价比
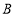种商品每件的进价多20元，用3000元购进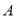种商品和用1800元购进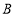种商品的数量相同．商店将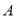种商品每件的售价定为80元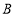，种商品每件的售价定为45元．（1）
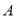种商品每件的进价和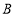种商品每件的进价各是多少元？（2）商店计划用不超过1560元的资金购进
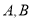两种商品共40件，其中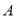种商品的数量不低于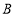种商品数量的一半，该商店有几种进货方案？（3）端午节期间，商店开展优惠促销活动，决定对每件
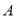种商品售价优惠
（
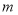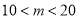）元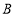，种商品售价不变，在（2）条件下，请设计出销售这40件商品获得总利润最大的进货方案．
相关试题
