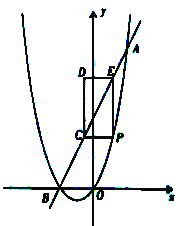
【题目】(2016贵州省毕节市第27题)如图,已知抛物线![]() 与直线
与直线![]() 交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作
交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线与直线AB交于点C和点E.
轴的平行线与直线AB交于点C和点E.
(1)求抛物线的解析式;
(2)若C 为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式。
参考答案:
【答案】(1)、y=![]() +2x;(2)、
+2x;(2)、![]() -1;(3)、
-1;(3)、![]() -4n-8m-16=0
-4n-8m-16=0
【解析】
试题分析:(1)、首先根据点A在一次函数上求出点A的坐标,然后代入二次函数得出解析式;(2)、根据一次函数和二次函数得出点B的坐标,根据中点的性质得出点C的坐标,根据点P在抛物线上得出点P的坐标,从而得出PC的长度;(3)、根据点D的坐标从而得出点C、点E和点P的坐标,根据DE=CP得出m和n之间的关系式.
试题解析:(1)、∵A(a,8)在直线上 ∴8=2a+4 解得:a=2
将A(2,8)代入二次函数可得:8=4+2b 解得:b=2 ∴抛物线的解析式为:y=![]() +2x
+2x
(2)、由 可得点B的坐标为(-2,0) 根据中点坐标公式可得:C(0,4)
可得点B的坐标为(-2,0) 根据中点坐标公式可得:C(0,4)
∵点P在抛物线上且纵坐标与C相同 ∴P(![]() -1,4) ∴PC=
-1,4) ∴PC=![]() -1-0=
-1-0=![]() -1.
-1.
(3)、∵D(m,n) ∴C(m,2m+4),E(![]() ,n),P(
,n),P(![]() ,2m+4)
,2m+4)
由DE=CP可得:![]() -m=
-m=![]() -m 化简得:
-m 化简得:![]() -4n-8m-16=0
-4n-8m-16=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图所示的图形,写出下列问题的结果:

(1)这个图形的名称是 ;
(2)这个几何体有 个面,有 个底面,有 个侧面,底面是 形,侧面是 形.
(3)侧面的个数与底面多边形的边数有什么关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有48名同学,在一次英语单词竞赛成绩统计中,成绩在81~ 90这一分数段的人数所占的频率是0.25,那么成绩在这个分数段的同学有_________名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016四川省乐山市第26题)如图1,二次函数
 的图象与
的图象与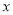 轴分别交于A、B两点,与
轴分别交于A、B两点,与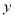 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程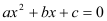 的两根为-8、2.
的两根为-8、2.(1)求二次函数的解析式;
(2)直线
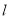 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,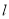 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.①求点P的运动路程;
②如图2,过点D作DE垂直
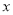 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在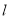 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;(3)在(2)的条件下,连结
 ,求△PEF周长的最小值.
,求△PEF周长的最小值.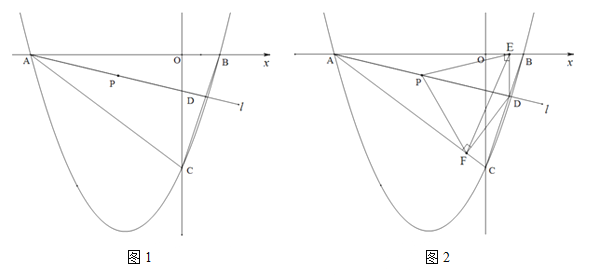
-
科目: 来源: 题型:
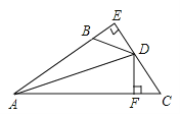
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.
(1)求证:AD平分∠BAC;(2)若AB=5,AC=9,则AE=_________.
相关试题

