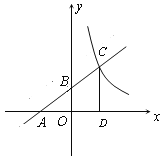
【题目】如图,已知一次函数![]() 的图像分别交x轴、y轴于A、B两点,且与反比例函数
的图像分别交x轴、y轴于A、B两点,且与反比例函数![]() (
( ![]() >0)的图像在第一象限交于点C(4,n),CD⊥x轴于D.
>0)的图像在第一象限交于点C(4,n),CD⊥x轴于D.
(1)求m、n的值;
(2)求△ADC的面积.
参考答案:
【答案】(1)m=3,n=6;(2)24.
【解析】试题分析:(1)、首先根据反比例函数解析式求出n的值,得出点C的坐标,然后将点C的坐标代入一次函数解析式求出m的值;(2)、首先根据一次函数解析式求出点A的坐标,从而得出AD和CD的长度,最后根据三角形的面积计算法则得出面积.
试题解析:(1)∵点C(4,n)在![]() 的图象上, ∴n=6,∴C(4,6).
的图象上, ∴n=6,∴C(4,6).
∵点C(4,6)在![]() 的图象上,∴m=3.
的图象上,∴m=3.
(2)∵C点和D点的坐标分别为(4,6)、(4,0),
直线![]() 与x轴的交点A的坐标为(-4,0),
与x轴的交点A的坐标为(-4,0),
∴AD=8,CD=6.
△ADC的面积为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式 A与2x的积为2x2+14x ,则A= ________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣5x+1=0的根的情况是( )
A.有两个不相等的实数根B.有两个相等的实数根
C.无实数根D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】
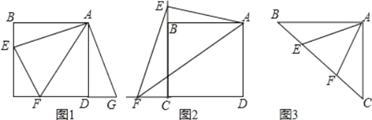
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3a2b·A=12a5b4+9a4b3-6a3b3-3a2b2 ,则A= ________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】雅安地震发生后,全国人民抗震救灾,众志成城,在地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(3,﹣2)关于原点对称点的坐标是( )
A.(3,2)
B.(﹣3,﹣2)
C.(﹣3,2)
D.(3,﹣2)
相关试题

