【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地为y1(km),快车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km),y1 ,y2与x的函数关系图像如图①所示,s与x的函数关系图如图②所示:
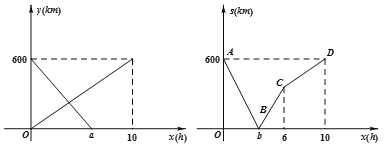
图① 图②
(1)图中的a= ,b= .
(2)求s关于x的函数关系式.
(3)甲、乙两地间有E、F两个加油站,相距200km,若慢车进入加油站E时,快车恰好进入加油站F,请直接写出加油站E到甲地的距离.
参考答案:
【答案】(1)6; ![]() ;(2)
;(2)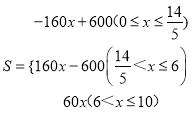 ;(3)加油站E到甲地的距离为300千米或450千米.
;(3)加油站E到甲地的距离为300千米或450千米.
【解析】(1)根据S与x之间的函数关系式可以得到当位于C点时,两车之间的距离增加变缓,此时快车到站,指出此时a的值即可,求得a的值后求出两车相遇时的时间即为b的值;
(2)根据函数的图象可以得到A、B、C、D的点的坐标,利用待定系数法求得函数的解析式即可.
(3)分两车相遇前和两车相遇后两种情况讨论,当相遇前令s=200代入直线AB解析式,当相遇后令s=200代入直线BC解析式即可求得x的值.
解:(1)由S与x之间的函数的图象可知:当位于C点时,两车之间的距离增加变缓,
∴由此可以得到a=6,
∴快车每小时行驶100千米,慢车每小时行驶60千米,两地之间的距离为600,
∴b=600÷(100+60)= ![]() ;
;
(2)∵从函数的图象上可以得到A、B、C、D点的坐标分别为:(0,600)、(![]() ,0)、(6,360)、(10,600),
,0)、(6,360)、(10,600),
∴设线段AB所在直线解析式为:S=kx+b,
∴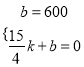 ,
,
解得:k=160,b=600,
设线段BC所在的直线的解析式为:S=kx+b,
∴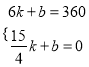
解得:k=160,b=600,
设直线CD的解析式为:S=kx+b,
∴![]() ,
,
解得:k=60,b=0
∴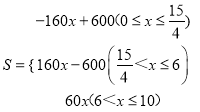 ;
;
(3)当两车相遇前分别进入两个不同的加油站,
此时:S=160x+600=200,
解得:x=![]() ,
,
当两车相遇后分别进入两个不同的加油站,
此时:S=160x600=200,
解得:x=5,
∴当x=![]() 或5时,此时E加油站到甲地的距离为450km或300km.
或5时,此时E加油站到甲地的距离为450km或300km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分).
(1)开始上课后第5分钟时与第30分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD的两条对角线相交于O,∠AOD=120°,AB=4cm,求矩形对角线的长和矩形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD是一块草坪,量得四边长AB=3m,BC=4m,DC=12m,AD=13m,∠B=90°,求这块草坪的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(a,-1)和N(2,b)不重合.
(1)当点M,N关于__对称时,a=2,b=1;
(2)当点M,N关于原点对称时,a=__,b=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
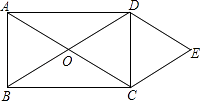
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若x=-2是方程8+2x=ax的解,则a=_______.
相关试题

