【题目】如图1,点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,且MN//PQ.
上一点,且MN//PQ.![]() 和
和![]() 的平分线交于点
的平分线交于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作直线交
作直线交![]() 于点
于点![]() (不与点
(不与点![]() 重合),交
重合),交![]() 于点E,
于点E,
①若点![]() 在点
在点![]() 的右侧,如图2,求证:
的右侧,如图2,求证:![]() ;
;
②若点![]() 在点
在点![]() 的左侧,则线段
的左侧,则线段![]() 、
、![]() 、
、![]() 有何数量关系?直接写出结论,不说理由.
有何数量关系?直接写出结论,不说理由.

参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1) 由平行线性质可得∠NAB+∠ABQ=180°,再由角平分线定义可得![]() ,再利用三角形内角和定理即可得∠C=90°,即可证明BC⊥AC;
,再利用三角形内角和定理即可得∠C=90°,即可证明BC⊥AC;
(2) ①延长AC交PQ点F,先证明AC=FC,再证明△ACD≌△FCE,即可得AD+BE=AB;
②方法与①相同.
解:(1)∵MN∥PQ
∴∠NAB+∠ABQ=180°
∵AC平分∠NAB,BC平分∠ABQ
∴![]()
∴∠BAC+∠ABC=![]() =90°
=90°
在△ABC中,∵∠BAC+∠ABC+∠C=180°
∴∠C=180°- (∠BAC+∠ABC) =180°-90°=90°
∴BC⊥AC;
(2)①延长AC交PQ于点F
∵BC⊥AC
∴∠ACB=∠FCB=90°
∵BC平分∠ABF
∴∠ABC=∠FBC
∴BC=BC
∴△ABC≌△FBC
∴AC=CF,AB=BF
∵MN∥BQ
∴∠DAC=∠EFC
∵∠ACD=∠FCE
∴△ACD≌△FCE
∴AD=EF
∴AB=BF=BE+EF=BE+AD
即:AB=AD+BE
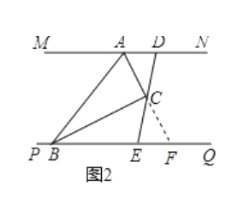

②线段AD,BE,AB数量关系是:AD+AB=BE
如图3,延长AC交PQ点F,
∵MN//PQ .
∴∠AFB=∠FAN,∠DAC=∠EFC
∵AC平分∠NAB
∴∠BAF=∠FAN
∴∠BAF=∠AFB
∴AB=FB
∵BC⊥AC
∴C是AF的中点
∴AC=FC
在△ACD与△FCE中
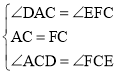
∴![]()
∴AD=EF
∵AB=FB=BE-EF
∴AD+AB=BE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.

(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】将长为
 ,宽为
,宽为 的长方形白纸,,按图所示的方法粘合起来,粘合部分的宽为
的长方形白纸,,按图所示的方法粘合起来,粘合部分的宽为 厘米.
厘米.
(1)根据题意,将表格补充完整.
白纸张数





……
纸条长度

_______


_______
……
(2)设
 张白纸粘合后的总长度为
张白纸粘合后的总长度为 厘米,写出
厘米,写出 与
与 之间的关系式;并求出
之间的关系式;并求出 张白纸粘合后的总长度.
张白纸粘合后的总长度.(3)若粘合后的总长度为
 ,问需要多少张白纸?
,问需要多少张白纸? -
科目: 来源: 题型:
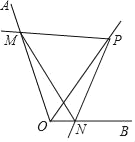
查看答案和解析>>【题目】如图,点P为定角∠AOB的平分线上的一个定点,点M,N分别在射线OA,OB上(都不与点O重合),且∠MPN与∠AOB互补.若∠MPN绕着点P转动,那么以下四个结论:①PM=PN恒成立;②MN的长不变;③OM+ON的值不变;④四边形PMON的面积不变.其中正确的为_____.(填番号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】早晨
 点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离
点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离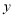 (千米)与他离校的时间
(千米)与他离校的时间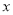 (小时)之间的图象.根据图象,完成下面问题:
(小时)之间的图象.根据图象,完成下面问题:(1)小明乘车去保护区的速度是_________千米/小时,
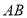 线段所表示的
线段所表示的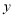 与
与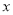 的关系式是_________;
的关系式是_________;(2)已知下午
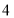 点,小明距保护区
点,小明距保护区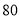 千米,问他何时才能回到学校?
千米,问他何时才能回到学校?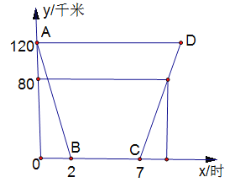
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形
 中,
中, ,
, ,
, ,
, 是
是 边上的中线,过点
边上的中线,过点 作
作 垂足为
垂足为 ,
, 交线段
交线段 于点
于点 ,交
,交 于点
于点 ,连接
,连接 .
.(1)求证:
 ;
;(2)探索线段
 和
和 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;(3)当
 等于多少度时,点
等于多少度时,点 恰好为
恰好为 中点?
中点?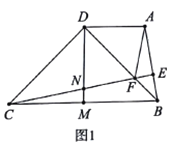
相关试题

