【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(-1,0);
⑤当1<x<4时,有y2<y1,

其中正确的是( ).
A. 5个 B. 4个 C. 3个 D. 2个
参考答案:
【答案】C
【解析】利用轴对称是直线y=1判定①;利用开口方向,对称轴与y主的交点判定a、b、c得出②;利用顶点坐标和平移的规律判定③;利用对称轴和二次函数的对称判定④;利用图象直接判定⑤即可.
解:∵对称轴x=-![]() =1‘∴2a+b=0,①正确;
=1‘∴2a+b=0,①正确;
∵a<0,∴b >0,∵抛物线与y轴的交点在正半轴上,∴c>0,∴abc<0,②错误;
∵把抛物线y=ax2+bx+c向下平移3个单位,得到y=ax2+bx-3,∴顶点坐标A(1,3)变为(1,0),抛物线与x轴相切,∴方程ax2+bx+c=3有两个相等的实数根,③正确;
∵对称轴是直线x=1,与x轴的一个交点是(4,0),∴与x轴的另一个交点是(-2,0),④错误;∵1<x<4时,由图象可知y2<y1,∴⑤正确.
正确的有①③⑤.
故选C.
“点睛”本题考查了二次项系数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△ADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为( )

A. 45°,90° B. 90°,45° C. 60°,30° D. 30°,60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某公司员工的年工资情况,小王随机调查了10位员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司年工资中等水平的是( )
A.方差
B.众数
C.中位数
D.平均数 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,一次函数y=ax+c和二次函数y=a(x+c)2的图象大致为( )
A.
 B.
B. 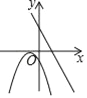 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1) 2a2-18
(2) -2x2y+8xy-8y
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为
 米.
米.(1)花圃的面积为____
 (用含
(用含 的式子表示);
的式子表示);(2)如果通道所占面积是整个长方形空地面积的
 ,求出此时通道的宽;
,求出此时通道的宽;(3)已知某园林公司修建通道、花圃的造价
 (元)、
(元)、 (元)与修建面积
(元)与修建面积
 之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价为105920元
之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价为105920元 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在旧城改造中,要拆除一建筑物AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在从离点B 24 m远的建筑物CD的顶端C测得点A的仰角为45°,点B的俯角为30°,问离点B 35 m处的一保护文物是否在危险区内?

相关试题

