【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ 。
_________ 。
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值。
的值。
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式。
的形式。
(5)解方程:x2 - 2x +4 = 0
参考答案:
【答案】(1) -i , 1 ;(2) 5 , 3+4i ; (3)x=-1,y=2
(4) i (5)x1= ![]() i , x2=
i , x2=![]() i
i
【解析】试题分析:(1)根据同底数幂的乘法法则、i2=﹣1计算即可;
(2)利用平方差公式、完全平方公式把原式展开,根据i2=﹣1计算即可;
(3)根据复数相等的条件解答即可;
(4)充分利用i2=﹣1计算,分子分母同时乘以(1+i)即可;
(5)计算出△=-3,根据虚数单位的定义即可求解.
试题解析:解:(1)i3=i2×i=-i,i4=(i2)2=(﹣1)2=1,故答案为:﹣i; 1;
(2)①(2+i)(2-i)=4-i2=4+1=5;
②(2+i)2=i2+4i+4=﹣1+4i+4=3+4i;
(3)根据复数相等的条件,得: ![]() ,解得:
,解得: ![]() ;
;
(4)![]() =
=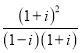 =
=![]() =
=![]() =i;
=i;
(5)x2﹣2x+4=0,x=![]() =
=![]() =
=![]() ,x1=
,x1= ![]() ,x2=
,x2= ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:

(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.


请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
-
科目: 来源: 题型:
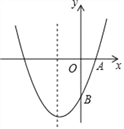
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
-
科目: 来源: 题型:
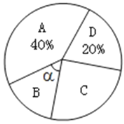
查看答案和解析>>【题目】2019年10月,某市高质量通过全国文明城市测评,该成绩的取得得益于领导高度重视(A)、整改措施有效(B)、市民积极参与(C)、市民文明素质(D).某数学兴趣小组随机走访了部分市民,对这四项认可度进行调查(只选填最认可的一项),并将调查结果制作了如下两幅不完整的统计图.
(1)请补全D项的条形图;
(2)已知B、C两项条形图的高度之比为3:5.
①选B、C两项的人数各为多少个?
②求α的度数,

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


-
科目: 来源: 题型:
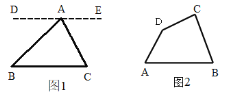
查看答案和解析>>【题目】(1)我们知道“三角形三个内角的和为 180°”.现在我们用平行线的性质来证明这个结论是正确的.
已知:∠BAC、∠B、∠C 是△ABC 的三个内角,如图 1.
求证:∠BAC+∠B+∠C=180° 证明:过点 A 作直线 DE∥BC(请你把证明过程补充完整)
(2)请你用(1)中的结论解答下面问题:
如图 2,已知四边形 ABCD,求∠A+∠B+∠C+∠D 的度数.
相关试题

