搜索
【题目】（1）我们知道“三角形三个内角的和为 180°”．现在我们用平行线的性质来证明这个结论是正确的．
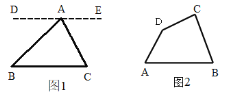
已知：∠BAC、∠B、∠C 是△ABC 的三个内角，如图 1．
求证：∠BAC+∠B+∠C=180° 证明：过点 A 作直线 DE∥BC（请你把证明过程补充完整）
（2）请你用（1）中的结论解答下面问题：
如图 2，已知四边形 ABCD，求∠A+∠B+∠C+∠D 的度数.
参考答案：
【答案】（1）详见解析 ；（2）360°
【解析】
（1）根据平行线性质和平角定义可得；（2）由（1）结论，连接AC.得到两个三角形△ABC和△ADC.
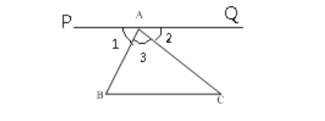
（1）证明：过点A作PQ∥BC
∴∠1=∠B(两直线平行,内错角相等)
∠2=∠C(两直线平行,内错角相等)
又∵∠1+∠2+∠3=180° (平角的定义)
∴∠BAC+∠B+∠C=180° (等量代换)
（2）连接AC.得到两个三角形△ABC和△ADC
∵三角形内角和是180°,所以两个就是360°.
∴∠A+∠B+∠C+∠D=360°
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：如果一个数的平方等于
，记为
,这个数
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数，表示为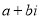
（
为实数），
叫这个复数的实部， 
叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似。例如计算：
（1）填空：
=_________, 
=____________.（2）填空：①
_________； ②
_________ 。（3）若两个复数相等，则它们的实部和虚部必须分别相等，完成下列问题：已知，
，（ 
为实数），求
的值。（4）试一试：请利用以前学习的有关知识将
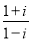化简成
的形式。（5）解方程：x2 - 2x +4 = 0
-
科目： 来源： 题型：
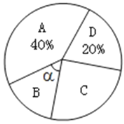
查看答案和解析>>【题目】2019年10月，某市高质量通过全国文明城市测评，该成绩的取得得益于领导高度重视（A）、整改措施有效（B）、市民积极参与（C）、市民文明素质（D）．某数学兴趣小组随机走访了部分市民，对这四项认可度进行调查（只选填最认可的一项），并将调查结果制作了如下两幅不完整的统计图．
（1）请补全D项的条形图；
（2）已知B、C两项条形图的高度之比为3：5．
①选B、C两项的人数各为多少个？
②求α的度数，
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
的图象过点C（0，1），顶点为Q（2，3）,点D在x轴正半轴上，线段OD=OC.（1）求抛物线的解析式；
（2）抛物线上是否存在点M，使得⊿CDM是以CD为直角边的直角三角形？若存在，请求出M点的坐标；若不存在，请说明理由.
（3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，,连接QE.若点P是线段QE上的动点，点F是线段OD上的动点，问：在P点和F点的移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，CD⊥AB于点D，DA=DC=4，DB=2，AF⊥BC于点F，交DC于点E．
（1）求线段AE的长；
（2）若点G是AC的中点，点M是线段CD上一动点，连结GM，过点G作GN⊥GM交直线AB于点N，记△CGM的面积为S1，△AGN的面积为S2．在点M的运动过程中，试探究：S1与S2的数量关系
-
科目： 来源： 题型：
查看答案和解析>>【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇，下表是近两周的销售情况：
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
（进价、售价均保持不变，利润=销售收入﹣进货成本）
（1）求A、B两种型号的电风扇的销售单价；
（2）若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，商场销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD．
（1）求点C，D的坐标及四边形ABDC的面积S四边形ABDC；
（2）在y轴上是否存在一点P，连接PA，PB，使S△PAB=S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由；
（3）点P是直线BD上一个动点，连接PC、PO ，当点P在直线BD上运动时，请直接写出∠OPC与∠PCD、∠POB的数量关系
相关试题
