【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.

(1)已知:如图1,四边形ABCD的顶点A,B,C在网格格点上,请你在如下的5![]() 7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
(2)如图2,矩形ABCD中,AB=![]() ,BC=5,点E在BC边上,连结DE画AF
,BC=5,点E在BC边上,连结DE画AF![]() DE于点F,若DE=
DE于点F,若DE=![]() CD,找出图中的等邻边四边形;
CD,找出图中的等邻边四边形;
(3)如图3,在Rt![]() ABC中,
ABC中,![]() ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
参考答案:
【答案】(1)见解析;(2)四边形ABEF和四边形ABED都是等邻边四边形;(3)当BM为2或3或![]() 时,四边形ACDM是“等邻边四边形”.
时,四边形ACDM是“等邻边四边形”.
【解析】
(1)根据”等邻边四边形”的定义画出3个不同形状的等邻边四边形;
(2)根据题意求出DE,根据勾股定理求出CE,计算得到BE=AB,根据等邻边四边形的定义判断即可;
(3)分AM=AC、DM=DC、MA=MD三种情况,根据勾股定理、等腰三角形的性质计算即可.
(1)3个不同形状的等邻边四边形ABCD如图所示:

(2)四边形ABEF和四边形ABED都是等邻边四边形,
∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=![]() ,
,
∴DE=![]() CD=
CD=![]() ,
,
由勾股定理得,CE=![]() =
=![]() ,
,
∴BE=BC-CE=5-![]() =
=![]() ,
,
∴BE=AB,
∴四边形ABEF和四边形ABED都是等邻边四边形;
(3)①当AM=AC时,BM=2;
②当DM=DC时,如图3,作DH⊥AB于H,

∵∠ACB=90°,AB=4,AC=2,
∴BC=![]() ,∠B=30°,
,∠B=30°,
∴BD=DM=![]() ,
,
在Rt△BDH中,BH=BD×cosB=![]() ,
,
∵DM=DB,DH⊥AB,
∴BM=2BH=3;
③当MA=MD时,如图4,作DH⊥AB于H,

设MA=MD=x,
由②得,BH=![]() ,DH=
,DH=![]() ,
,
则MH=4-x-![]() =
=![]() -x,
-x,
在Rt△MDH中,DM2=MH2+DH2,即x2=(![]() -x)2+(
-x)2+(![]() )2,
)2,
解得,x=![]() ,即AM=
,即AM=![]() ,
,
∴BM=4-![]() =
=![]() ,
,
综上所述,当BM为2或3或![]() 时,四边形ACDM是“等邻边四边形”.
时,四边形ACDM是“等邻边四边形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.(1)求此抛物线的解析式;
(2)过点E作EG⊥AB于点G,Q为线段AC的中点,当△EGF周长最大时,在
 轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
(3)在(2)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.

-
科目: 来源: 题型:
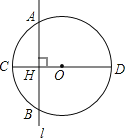
查看答案和解析>>【题目】如图,⊙O的半径OC=10cm,直线l⊥CO,垂足为H,交⊙O于A,B两点,AB=16cm,直线l平移多少厘米时能与⊙O相切?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程:x
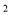 ﹣2x﹣8=0,解决一下问题:
﹣2x﹣8=0,解决一下问题:(1)不解方程判断此方程的根的情况;
(2)请按要求分别解这个方程:①配方法;②因式分解法.
(3)这些方法都是将解 转化为解 ;
(4)尝试解方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是
 .
.(1)求暗箱中红球的个数;
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
-
科目: 来源: 题型:
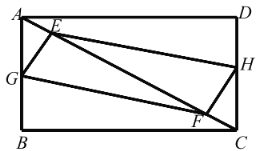
查看答案和解析>>【题目】在矩形 ABCD 中,AB=3,BC=4,E、F 是对角线 AC 上的两个动点,分 别从 A、C 同时出发相向而行,速度均为每秒 1 个单位长度,运动时间为 t 秒,其中 0 t 5 .
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 是平行四边形(E、F 相遇时除外);
(2)在(1)条件下,若四边形 EGFH 为矩形,求 t 的值;
(3)若 G,H 分别是折线 A-B-C,C-D-A 上的动点,与 E,F 相同的速度同时出发,若 四边形 EGFH 为菱形,求 t 的值.
相关试题

