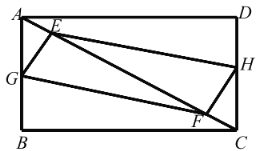
【题目】在矩形 ABCD 中,AB=3,BC=4,E、F 是对角线 AC 上的两个动点,分 别从 A、C 同时出发相向而行,速度均为每秒 1 个单位长度,运动时间为 t 秒,其中 0 t 5 .
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 是平行四边形(E、F 相遇时除外);
(2)在(1)条件下,若四边形 EGFH 为矩形,求 t 的值;
(3)若 G,H 分别是折线 A-B-C,C-D-A 上的动点,与 E,F 相同的速度同时出发,若 四边形 EGFH 为菱形,求 t 的值.
参考答案:
【答案】(1)见解析;(2)0.5或4.5;(3)![]()
【解析】
(1)根据勾股定理求出AC,证明△AFG≌△CEH,根据全等三角形的性质得到GF=HE,同理得到GE=HF,根据平行四边形的判定定理证明;
(2)分AE=CF、AE=CF两种情况,根据矩形的性质计算即可;
(3)连接AG、CH,判定四边形AGCH是菱形,得到AG=CG,根据勾股定理求出BG,得到AB+BG的长,根据题意解答.
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=![]() ,∠GAF=∠HCE,
,∠GAF=∠HCE,
∵G,H分别是AB,DC中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG和△CEH中,
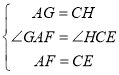 ,
,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形;
(2)解:由(1)得:BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=4,当EF=GH=4时,平行四边形EGFH是矩形,
分两种情况:①AE=CF=t,EF=5-2t=4,
解得:t=0.5;
②AE=CF=t,EF=5-2(5-t)=4,
解得:t=4.5;
综上所述:当t为0.5s或4.5s时,四边形EGFH为矩形;
(3)解:连接AG、CH,如图所示:
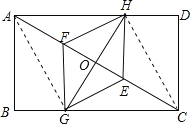
∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH,OE=OF,
∴OA=OC,AG=AH,
∴四边形AGCH是菱形,
∴AG=CG,
设AG=CG=x,则BG=4-x,
由勾股定理得:AB2+BG2=AG2,
即32+(4-x)2=x2,
解得,x=![]() ,
,
∴BG=![]() =
=![]() ,
,
∴AB+BG=3+![]() =
=![]() ,
,
∴t为![]() 时,四边形EGFH为菱形.
时,四边形EGFH为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.

(1)已知:如图1,四边形ABCD的顶点A,B,C在网格格点上,请你在如下的5
 7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;(2)如图2,矩形ABCD中,AB=
 ,BC=5,点E在BC边上,连结DE画AF
,BC=5,点E在BC边上,连结DE画AF DE于点F,若DE=
DE于点F,若DE= CD,找出图中的等邻边四边形;
CD,找出图中的等邻边四边形;(3)如图3,在Rt
 ABC中,
ABC中, ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是
 .
.(1)求暗箱中红球的个数;
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
-
科目: 来源: 题型:
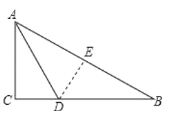
查看答案和解析>>【题目】如图,有一块直角三角形纸片,AC=6,BC=8,现将△ABC沿直线AD折叠,使AC落在斜边AB上,且C与点E重合,则AD的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax
 +bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

