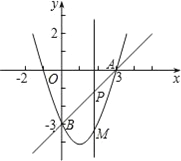
【题目】如图，在平面直角坐标系中，抛物线y=x2+mx+n经过点A（3，0）、B（0，﹣3），点P是直线AB上的动点，过点P作x轴的垂线交抛物线于点M，设点P的横坐标为t．

（1）分别求出直线AB和这条抛物线的解析式．

（2）若点P在第四象限，连接AM、BM，当线段PM最长时，求△ABM的面积．

（3）是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请求出点P的横坐标；若不存在，请说明理由．

参考答案：

【答案】（1）抛物线的解析式是y=，直线AB的解析式是y=x-3；

（2）；

（3）存在，P点的横坐标是或；

【解析】试题分析：（1）分别利用待定系数法求两函数的解析式：把A（3，0）B（0，﹣3）分别代入与，得到关于m、n的两个方程组，解方程组即可；

（2）设点P的坐标是（， ），则M（， ），用P点的纵坐标减去M的纵坐标得到PM的长，即PM=（）﹣（）=，然后根据二次函数的最值得到

当时，PM最长为，再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可；

（3）由PM∥OB，根据平行四边形的判定得到当PM=OB时，点P、M、B、O为顶点的四边形为平行四边形，然后讨论：当P在第四象限：PM=OB=3，PM最长时只有，所以不可能；当P在第一象限：PM=OB=3，（ ）﹣（）=3；当P在第三象限：PM=OB=3， ，分别解一元二次方程即可得到满足条件的t的值．

试题解析：（1）把A（3，0）B（0，﹣3）代入，得： ，解得，

所以抛物线的解析式是．

设直线AB的解析式是，

把A（3，0）B（0，﹣3）代入，得： ，解得： ，

所以直线AB的解析式是；

（2）设点P的坐标是（， ），则M（， ），因为p在第四象限，

所以PM=（）﹣（）=，

当时，二次函数的最大值，即PM最长值为，

则S△ABM=S△BPM+S△APM=；

（3）存在，理由如下：∵PM∥OB，

∴当PM=OB时，点P、M、B、O为顶点的四边形为平行四边形，

①当P在第四象限：PM=OB=3，PM最长时只有，所以不可能有PM=3．

②当P在第一象限：PM=OB=3，（ ）﹣（）=3，解得， （舍去），所以P点的横坐标是；

③当P在第三象限：PM=OB=3， ，解得（舍去），，所以P点的横坐标是．所以P点的横坐标是或．

关闭