【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
如图延长EF交BC的延长线于G,取AB的中点H连接FH.证明△DFE≌△FCG 得EF=FG,BE⊥BG,四边形BCFH是菱形即可解决问题;
如图延长EF交BC的延长线于G,取AB的中点H连接FH.
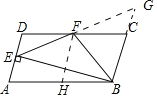
∵CD=2AD,DF=FC,
∴CF=CB,
∴∠CFB=∠CBF,
∵CD∥AB,
∴∠CFB=∠FBH,
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确,
∵DE∥CG,
∴∠D=∠FCG,
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△FCG,
∴FE=FG,
∵BE⊥AD,
∴∠AEB=90°,
∵AD∥BC,
∴∠AEB=∠EBG=90°,
∴BF=EF=FG,故②正确,
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故③正确,
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC,
∴四边形BCFH是菱形,
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故④正确,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.
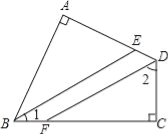
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中
 ,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D(1) 当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
(2) 当直线MN绕点O旋转到图②的位置时,求证:CD=AC-BD;
(3) 当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A.
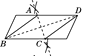 B.
B. 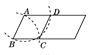 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AC=6,BD=8,求线段OE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示.

(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到F,使CF=CE,连接DF.若CE=1 cm,则BF=__________.

相关试题

