【题目】我校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”。请你指出哪位同学的调查方式最合理:
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图。

请你根据以上图表提供的信息解答下列问题:
① a= , b= ;
②在扇形统计图中器乐类所对应扇形的圆心角的度数是 ;
③若我校七年级有学生480人,请你估计大约有多少学生参加武术类校本课程。
参考答案:
【答案】(1)丙同学的说法最合理;(2)① 100,0.15;② 144°;③ 120
【解析】试题分析:(1)采用随机调查的方式比较合理,随机调查的关键是调查的随机性,这样才合理;
(2)①用喜欢书画类的频数除以喜欢书画类的频率即可求得a值,用喜欢棋牌类的人数除以总人数即可求得b值.
②求得器乐类的频率乘以360°即可.
③用总人数乘以喜欢书画类的频率即可求参加书画类校本课程的总人数.
试题解析:(1)∵调查的人数较多,范围较大,
∴应当采用随机抽样调查,
∵到六年级每个班随机调查一定数量的同学相对比较全面,
∴丙同学的说法最合理.
(2)①∵喜欢武术类的有25人,百分比为25%,
∴总人数=25÷0.25=100,喜欢书画类的有100-25-15-40=20人,
棋牌类的百分比为15÷100=0.15.
②∵喜欢器乐类的频率为:1-0.25-0.20-0.15=0.4,
∴喜欢器乐类所对应的扇形的圆心角的度数为:360×0.4=144°,
③参加书画类校本课程人数为:480×0.25=120(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度数;
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)【问题情境】
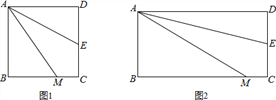
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】(1)证明:AM=AD+MC;
【拓展延伸】(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)中的结论是否成立?请作出判断,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)直线y=x﹣6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF∥AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x﹣6与坐标轴交点坐标是A( , ),B( , );
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

-
科目: 来源: 题型:
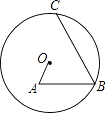
查看答案和解析>>【题目】如图所示,在⊙O内有折线OABC,其中OA=4,AB=6,∠A=∠B=60°,则BC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=10cm,AM=3cm,求CN的长;
(2)如果MN=6cm,求AB的长.

相关试题

