搜索
【题目】如图所示，在⊙O内有折线OABC，其中OA=4，AB=6，∠A=∠B=60°，则BC的长为 ．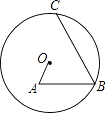 
参考答案：
【答案】10
【解析】解：延长AO交BC于D，作OH⊥BC于H， ∵∠A=∠B=60°，
∴△ABD为等边三角形，
∴∠ADB=60°，AD=BD=AB=6，
∴OD=AD﹣OA=6﹣4=2，
在Rt△ODH中，∠ODH=60°，
∴∠DOH=30°，
∴DH= 
OD=1，
∴BH=BD﹣DH=6﹣1=5，
∵OH⊥BC，
∴BC=2BH=10．
故答案为：10．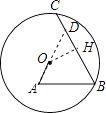
首先延长AO交BC于D，作OH⊥BC于H，由∠A=∠B=60°，可判断△ABD为等边三角形，根据等边三角形的性质可求得BD的长，再由含30°角的直角三角形的性质，求得DH的长，则可得到BH的长，根据垂径定理的性质，即可求得答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）直线y=x﹣6与x轴、y轴分别交于点A、B，点E从B点，出发以每秒1个单位的速度沿线段BO向O点移动（与B、O点不重合），过E作EF∥AB，交x轴于F．将四边形ABEF沿EF折叠，得到四边形DCEF，设点E的运动时间为t秒．
（1）①直线y=x﹣6与坐标轴交点坐标是A（ ， ），B（ ， ）；
②画出t=2时，四边形ABEF沿EF折叠后的图形（不写画法）；
（2）若CD交y轴于H点，求证：四边形DHEF为平行四边形；并求t为何值时，四边形DHEF为菱形（计算结果不需化简）；
-
科目： 来源： 题型：
查看答案和解析>>【题目】我校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数：
（1）确定调查方式时，甲同学说：“我到七年级（1）班去调查全体同学”；乙同学说：“放学时我到校门口随机调查部分同学”；丙同学说：“我到七年级每个班随机调查一定数量的同学”。请你指出哪位同学的调查方式最合理：
（2）他们采用了最为合理的调查方法收集数据，并绘制了如图所示的统计表和扇形统计图。
请你根据以上图表提供的信息解答下列问题：
① a= ， b= ;
②在扇形统计图中器乐类所对应扇形的圆心角的度数是 ；
③若我校七年级有学生480人，请你估计大约有多少学生参加武术类校本课程。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，A F∥CE，且交BC于点F．
（1）求证：△ABF≌△CDE；
（2）如图，若∠1=65°，求∠B的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C是线段AB上一点，M是线段AC的中点，N是线段BC的中点．
(1)如果AB＝10cm，AM＝3cm，求CN的长；
(2)如果MN＝6cm，求AB的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一只不透明的盒子里有背面完全相同，正面上分别写有数字1、2、3、4的四张卡片，小马从中随机地抽取一张，把卡片上的数字作为被减数；在另一只不透明的盒子里将形状、大小完全相同，分别标有数字1、2、3的三个小球混合后，小虎从中随机地抽取一个，把小球上的数字做为减数，然后计算出这两个数的差．
（1）请你用画树状图或列表的方法，求这两数差为0的概率；
（2）小马与小虎做游戏，规则是：若这两数的差为非正数，则小马赢；否则小虎赢．你认为该游戏公平吗？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，水坝的横断面是梯形，背水坡AB的坡角∠BAD=60°，坡长AB=20
m，为加强水坝强度，降坝底从A处后水平延伸到F处，使新的背水坡角∠F=45°，求AF的长度（结果精确到1米，参考数据： 
1.414， ≈1.732）．
相关试题
