【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案. 甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500 元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.
(1)求如图所示的y与x的函数解析式:(不要求写出定义域);
(2)如果某学校目前的绿化面积是1200平方米,试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
参考答案:
【答案】
(1)解:设y=kx+b,则有 ![]() ,解得
,解得 ![]() ,
,
∴y=5x+400
(2)解:绿化面积是1200平方米时,甲公司的费用为6400元,乙公司的费用为5500+4×200=6300元,
∵6300<6400
∴选择乙公司的服务,每月的绿化养护费用较少
【解析】(1)利用待定系数法即可解决问题;(2)绿化面积是1200平方米时,求出两家的费用即可判断;
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:一个正n边形(n为整数,n≥4)的最短对角线与最长对角线长度的比值叫做这个正n边形的“特征值”,记为λn , 那么λ6= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.

(1)当k=4时,求这条抛物线的解析式;
(2)当k=4时,求运动员落水点与点C的距离;
(3)图中CE= 米,CF=
米,CF=  米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.

(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
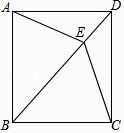
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.

(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
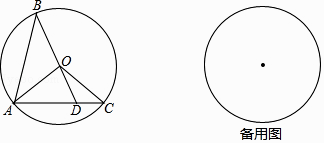
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离;
(3)记△AOB、△AOD、△COD 的面积分别为S1、S2、S3 , 如果S2是S1和S3的比例中项,求OD的长.
相关试题

