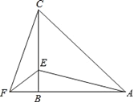
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=25°,求∠BFC度数.
参考答案:
【答案】
【1】 证明:∵∠ABC=90°,∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF, AB=BC,
∴Rt△ABE≌Rt△CBF(HL).---------------------4分
【2】 解:∵AB=BC, ∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-25°=20°,
由(1)得Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=20°,
∴∠ACF=∠BCF+∠ACB=45°+20°=65°. ---------------------8分
【解析】
(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB的两个端点坐标分别为A(1,1),B(2,1),以原点O为位似中心,将线段AB放大后得到线段CD.若CD=2,则端点C的坐标为( )

A.(2,2)
B.(2,4)
C.(3,2)
D.(4,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,E , F , G , H分别是OA , OB , OC , OD的中点,则正方形EFGH与正方形ABCD的面积比是( )

A.1:6
B.1:5
C.1:4
D.1:2 -
科目: 来源: 题型:
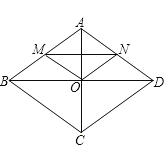
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC、BD相交于点O , M、N分别是边AB、AD的中点,连接OM、ON、MN , 则下列叙述正确的是( )
A.△AOM和△AON都是等边三角形
B.四边形MBON和四边形MODN都是菱形
C.四边形AMON和四边形ABCD都是位似图形
D.四边形MBCO和四边形NDCO都是等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )

A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,1),B(-2,0),以坐标原点O为位似中心,将线段AB放大2倍,放大后的线段A′B′与线段AB在同一侧,则两个端点A′,B′的坐标分别为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
相关试题

