【题目】在等腰△ABC中,
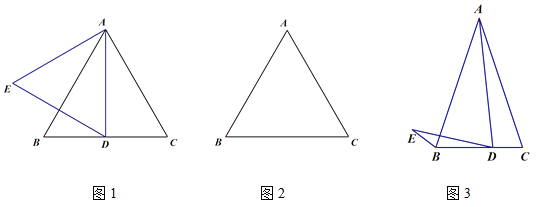
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为___________;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
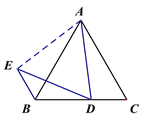
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
……
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的的数量关系,这个数量关系是______________________.(直接给出结论无须证明)
参考答案:
【答案】(1)30°;(2)答案见解析;(3)k(BE+BD)=AC
【解析】试题解析:(1)由AD是等边三角形ABC的BC边上的中线得AD⊥BC,由AE与AD关于AB对称,从而AB垂直平分DE,可得∠ADE=60°,所以∠BDE=30°;
(2)①根据题意画图即可;
②如思路1,证明△EAB≌△DAC即可得出结论.
(3)k(BE+BD)=AC.
试题解析:(1)∵ΔABC是等边三角形,D是BC边的中点
∴∠BAD=30°
∵线段AD和AE关于直线AB对称
∴DE⊥AB
∴∠ADE=60°
∴∠BDE=90°-60°=30°;
(2)作图如下:
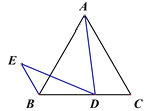
②如图,连接AE.
![]()
![]()
![]()
![]()
![]()
![]()
(3)k(BE+BD)=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列六种说法正确的个数是( )
①无限小数都是无理数;
②正数、负数统称实数;
③无理数的相反数还是无理数;
④无理数与无理数的和一定还是无理数;
⑤无理数与有理数的和一定是无理数;
⑥无理数与有理数的积一定仍是无理数.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中一条对角线分∠A为35°和45°,则∠B=______________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内的三条直线有哪几种位置关系?请画图说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=a,
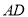 ∶DE=4∶1,写出求DE长的思路.
∶DE=4∶1,写出求DE长的思路.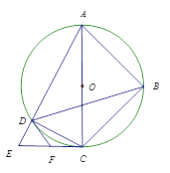
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )
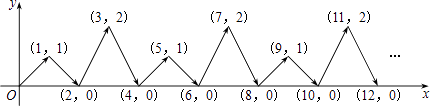
A.(2015,0)
B.(2015,1)
C.(2015,2)
D.(2016,0)
相关试题

