【题目】综合题
(1)发现
如图,点 ![]() 为线段
为线段 ![]() 外一动点,且
外一动点,且 ![]() ,
, ![]() .
.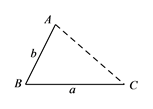
填空:当点 ![]() 位于时,线段
位于时,线段 ![]() 的长取得最大值,且最大值为.(用含
的长取得最大值,且最大值为.(用含 ![]() ,
, ![]() 的式子表示)
的式子表示)
(2)应用
点 ![]() 为线段
为线段 ![]() 外一动点,且
外一动点,且 ![]() ,
, ![]() .如图所示,分别以
.如图所示,分别以 ![]() ,
, ![]() 为边,作等边三角形
为边,作等边三角形 ![]() 和等边三角形
和等边三角形 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
①找出图中与 ![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段 ![]() 长的最大值.
长的最大值.
(3)拓展
如图,在平面直角坐标系中,点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]()
![]() 为线段
为线段 ![]() 外一动点,且
外一动点,且 ![]() ,
, ![]() ,
, ![]() ,求线段
,求线段 ![]() 长的最大值及此时点
长的最大值及此时点 ![]() 的坐标.
的坐标.
参考答案:
【答案】
(1)CB的延长线上,a+b
(2)解:①DC=BE,理由如下:
∵△ABD和△ACE为等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
∴△CAD≌△EAB.
∴DC=BE.
②BE的最大值是4.
(3)解:如图3,
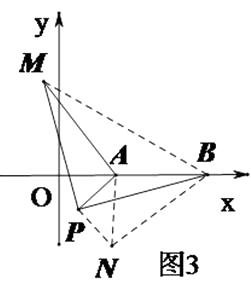
构造△BNP≌△MAP,则NB=AM,由(1)知,当点N在BA的延长线上时,NB有最大值(如备用图)。
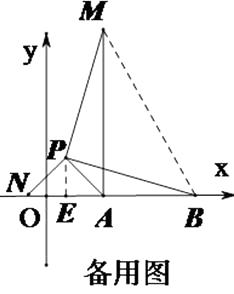
易得△APN是等腰直角三角形,AP=2,∴AN= ![]() ,∴AM=NB=AB+AN=3+
,∴AM=NB=AB+AN=3+ ![]() ;过点P作PE⊥x轴于点E,PE=AE=
;过点P作PE⊥x轴于点E,PE=AE= ![]() ,又A(2,0)∴P(2-
,又A(2,0)∴P(2- ![]() ,
, ![]() )
)
【解析】(1)当点A在线段CB的延长线上时,可得线段AC的长取得最大值为a+b;
(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论。
(2)①根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根据全等三角形的性质得到CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果。
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值;如图2,过P作PE⊥x轴于E,根据等腰直角三角形的性质即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形
 中,
中, 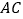 平分
平分 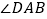 ,
, 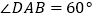 ,
, 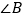 与
与 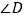 互补,
互补, 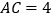 ,
, 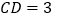 ,则
,则 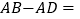 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形的三边长为6,8,x,则以x为边长的正方形的面积为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】35°42′﹣34°48′+60°30′= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 在函数
在函数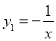 (
(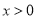 )的图象上,点
)的图象上,点 在直线
在直线 (
(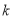 为常数,且
为常数,且 )上,若
)上,若 ,
, 两点关于原点对称,则称点
两点关于原点对称,则称点 ,
, 为函数
为函数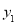 ,
,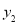 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为
图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为A.有
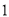 对或
对或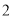 对 B.只有
对 B.只有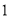 对 C.只有
对 C.只有 对 D.有
对 D.有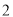 对或
对或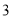 对
对 -
科目: 来源: 题型:
查看答案和解析>>【题目】上周六上午
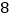 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离 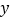 (千米)与他们路途所用的时间
(千米)与他们路途所用的时间  (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题: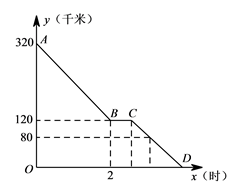
(1)求直线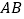 所对应的函数关系式;
所对应的函数关系式;
(2)已知小颖一家出服务区后,行驶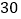 分钟时,距姥姥家还有
分钟时,距姥姥家还有  千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程x2+4x+a=0的两个不相等实数根x1 , x2满足x1x2﹣2x1﹣2x2﹣5=0,那么a的值为( )
A.3
B.﹣3
C.13
D.﹣13
相关试题

