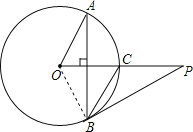
【题目】已知P是⊙O外一点，PO交⊙O于点C，OC=CP=2，弦AB⊥OC，∠AOC的度数为60°，连接PB．

（1）求BC的长；

（2）求证：PB是⊙O的切线．

参考答案：

【答案】（1）BC=2；（2）见解析

【解析】

试题分析：（1）连接OB，根据已知条件判定△OBC的等边三角形，则BC=OC=2；

（2）欲证明PB是⊙O的切线，只需证得OB⊥PB即可．

（1）解：如图，连接OB．

∵AB⊥OC，∠AOC=60°，

∴∠OAB=30°，

∵OB=OA，

∴∠OBA=∠OAB=30°，

∴∠BOC=60°，

∵OB=OC，

∴△OBC的等边三角形，

∴BC=OC．

又OC=2，

∴BC=2；

（2）证明：由（1）知，△OBC的等边三角形，则∠COB=60°，BC=OC．

∵OC=CP，

∴BC=PC，

∴∠P=∠CBP．

又∵∠OCB=60°，∠OCB=2∠P，

∴∠P=30°，

∴∠OBP=90°，即OB⊥PB．

又∵OB是半径，

∴PB是⊙O的切线．

关闭