【题目】【问题发现】
(1)如图(1),四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为__________;
【拓展探究】
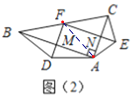
(2)如图(2),在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
【解决问题】
(3)如图(3),在正方形ABCD中,AB=2![]() ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.

参考答案:
【答案】(1)AC垂直平分BD(2)四边形FMAN是矩形(3)BD′的平方为16+8![]() 或16–8
或16–8![]()
【解析】试题分析:(1)根据AB=AD、CB=CD可知点A、C在线段BD的垂直平分线上,从而可得;
(2)连接AF,判断出DF是AB的垂直平分线,从而可得∠FMA=90![]() ,同理可得∠FNA=90
,同理可得∠FNA=90![]() ,再根据∠MAN=90
,再根据∠MAN=90![]() ,即可判断出四边形FMAN为矩形;
,即可判断出四边形FMAN为矩形;
(3)分逆时针旋转与顺时针旋转两种情况分别讨论即可得.
试题解析:(1)∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∵点A、点C是不同的点,
∴AC⊥BD,
故答案为:垂直;
(2)猜想:四边形FMAN是矩形,理由如下:
连接AF,在Rt△ABC中,∵点F为BC的中点,
![]() AF=BF,
AF=BF,
在等腰三角形ADB中,AD=BD,
![]() FD垂直平分AB,
FD垂直平分AB,![]() ∠FMA=90
∠FMA=90![]() ,
,
同理可得∠FNA=90![]() ,又∵∠MAN=90
,又∵∠MAN=90![]() ,
,
![]() 四边形FMAN为矩形;
四边形FMAN为矩形;
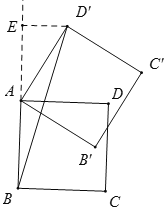
(3)当逆时针旋转60度时,如图,过点D′作D′⊥AB,交BA延长线于点E,
则有∠D′AE=30°,∴D′E=![]() AD′=1,AE=
AD′=1,AE=![]() ,
,
∴BE=![]() ,∴BD′2=BE2+ED′2=(
,∴BD′2=BE2+ED′2=(![]() )2+12=8+4
)2+12=8+4![]() ;
;
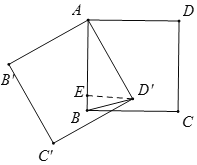
当顺时针旋转60度时,如图,过点D′作D′⊥AB,交BA于点E,
则有∠D′AE=30°,∴D′E=![]() AD′=1,AE=
AD′=1,AE=![]() ,
,
∴BE=![]() ,∴BD′2=BE2+ED′2=(
,∴BD′2=BE2+ED′2=(![]() )2+12=8-4
)2+12=8-4![]() ,
,
综上,BD′2的值为8+4![]() 或8-4
或8-4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
参考数据:
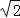 ≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.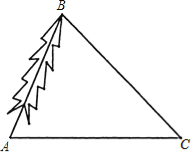
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的
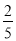 .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②-a<b;③a+b>0;④c-a<0;⑤a+c>0;⑥
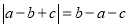 ;正确的个数有( )
;正确的个数有( )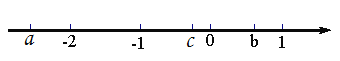
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.

相关试题

