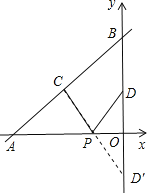
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() x+4中y=0,则
x+4中y=0,则![]() x+4=0,解得:x=-6,
x+4=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(-3,2),D′(0,-2),
∴有![]() ,解得:
,解得: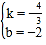 ,
,
∴直线CD′的解析式为y=-![]() x-2.
x-2.
令y=-![]() x-2中y=0,则0=-
x-2中y=0,则0=-![]() x-2,解得:x=-
x-2,解得:x=-![]() ,
,
∴点P的坐标为(-![]() ,0).
,0).
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,拦水坝的横断面为梯形ABCD,坝顶宽AD=5米,斜坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
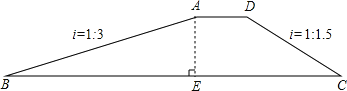
(1)求斜坡AB的长;
(2)求拦水坝的横断面梯形ABCD的周长.(注意:本题中的计算过程和结果均保留根号)
-
科目: 来源: 题型:
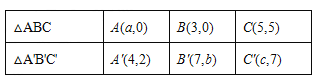
查看答案和解析>>【题目】已知△A'B'C'是由△ABC经过平移得到的,它们的顶点在平面直角坐标系中的坐标如下表所示:
(1)观察表中各对应点坐标的变化,并填空:
a= , b= ,c= ;
(2)在平面直角坐标系中画出△ABC及平移后的△A'B'C';(3)△A'B'C'的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )
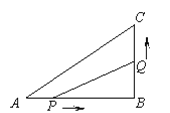
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=﹣
 x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
A. (0,3) B. (0,
 ) C. (0,
) C. (0, ) D. (0,
) D. (0, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙o的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

相关试题

