【题目】在一个不透明的盒子里装有三个分别写有数字6,﹣2,7的小球,它们的形状、大小、质地完全相同,先从盒子里随机抽取一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字,请你用画树状图或列表的方法求两次取出小球上的数字和大于10的概率.
参考答案:
【答案】解: 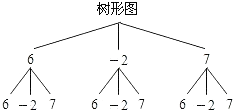
第二次 | 6 | ﹣2 | 7 |
6 | (6,6) | (6,﹣2) | (6,7) |
﹣2 | (﹣2,6) | (﹣2,﹣2) | (﹣2,7) |
7 | (7,6) | (7,﹣2) | (7,7) |
P(两数和大于10)= ![]()
【解析】解此题的关键是准确列表或画树形图,找出所有的可能情况,即可求得概率.
【考点精析】解答此题的关键在于理解列表法与树状图法的相关知识,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P到∠AOB的距离定义如下:点Q为∠AOB的两边上的动点,当PQ最小时,我们称此时PQ的长度为点P到∠AOB的距离,记为d(P,∠AOB).特别的,当点P在∠AOB的边上时,d(P,∠AOB)=0.在平面直角坐标系xOy中,A(4,0).

(1)如图1,若M(0,2),N(﹣1,0),则d(M,∠AOB)= , d(N,∠AOB)=;
(2)在正方形OABC中,点B(4,4).如图2,若点P在直线y=3x+4上,且d(P,∠AOB)=2 ,求点P的坐标;
,求点P的坐标;
(3)如图3,若点P在抛物线y=x2﹣4上,满足d(P,∠AOB)=2 的点P有个,请你画出示意图,并标出点P.
的点P有个,请你画出示意图,并标出点P. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y=
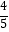 x上一点,则点B与其对应点B′间的距离为 .
x上一点,则点B与其对应点B′间的距离为 . 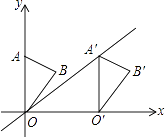
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某抛物线的对称轴为直线x=2,点E是该抛物线顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D,点A是对称轴上一点,连结AC、AB,若△ABC是等边三角形,则图中阴影部分图形的面积之和是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:

根据上述信息,解答下列问题:
(1)抽取的学生人数为;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,
 ≈1.414].
≈1.414].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD.
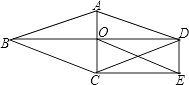
(1)试判断四边形OCED的形状,并说明理由;
(2)若AC=6,BD=8,求线段OE的长.
相关试题

