搜索
【题目】已知一次函数y=kx+b的图像经过点(－1.－5)，且与正比例函数y=
x的图象相交于点(2，m).
(1)求m的值；
(2)求一次函数y=kx+b的解析式；
(3)求这两个函数图像与x轴所围成的三角形面积.
参考答案：
【答案】(1)、m=1；(2)、y=2x－3；(3)、
【解析】
试题分析：(1)将点(2，m)代入正比例函数求出m的值；(2)将(－1，－5)和交点代入一次函数求出解析式；(3)、三角形的面积根据面积计算法则进行计算
试题解析：(1)、将(2，m)代入y=
x，得：m=2×=1
(2)、将(－1，－5)和(2,1)代入y=kx+b，
得：
解得：
即一次函数的解析式为：y=2x－3
(3)、一次函数与x轴的交点为(
，0) ∴S=×1÷2=
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种病毒繁殖非常快，每分钟会由1个繁殖到3个．
试问：经过4分钟，1个病毒会繁殖到多少个？若这些病毒继续繁殖，m分钟后会繁殖到多少个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若（x﹣3）2+|x﹣y+m|=0，当y＞0时，则m的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=x2﹣4x﹣3的顶点坐标为（ ）
A. （2，﹣7） B. （2，7） C. （﹣2，﹣7） D. （﹣2，7）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知CF⊥AB于F，ED⊥AB于D，∠1=∠2，求证：FG∥BC．
-
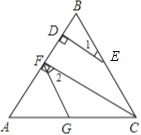
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+c（a≠0）经过A，B，C三点，点B的坐标为（-3，0），且OC=3OA，直线y=x+m经过B、C两点．
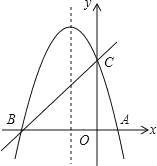
（1）求抛物线的解析式；
（2）在抛物线的对称轴上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为抛物线的对称轴上的一个动点，求使△BPC为直角三角形的点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：
（1）x2﹣4；
（2）x3﹣2x2+x．
相关试题
