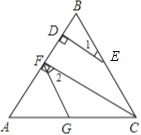
【题目】如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
参考答案:
【答案】依题意知,CF⊥AB于F,ED⊥AB于D,∴∠BDE=∠BFC=90°,则DE∥FC,∴∠1=∠BCF。
∵∠1=∠2(已知)∴∠BCF=∠2.∴FG∥BC(内错角相等,两直线平行)
【解析】试题分析:根据在同一平面内垂直于同一条直线的两条直线平行可知DE∥FC,故∠1=∠ECF=∠2.根据内错角相等两直线平行可知,FG∥BC.
证明:∵CF⊥AB,ED⊥AB,
∴DE∥FC(垂直于同一条直线的两条直线互相平行),
∴∠1=∠BCF(两直线平行,同位角相等);
又∵∠2=∠1(已知),
∴∠BCF=∠2(等量代换),
∴FG∥BC(内错角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣3)2+|x﹣y+m|=0,当y>0时,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4x﹣3的顶点坐标为( )
A. (2,﹣7) B. (2,7) C. (﹣2,﹣7) D. (﹣2,7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y=
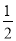 x的图象相交于点(2,m).
x的图象相交于点(2,m).(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.
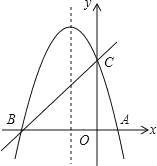
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴上的一个动点,求使△BPC为直角三角形的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)x2﹣4;
(2)x3﹣2x2+x. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a﹣ab=_____.
相关试题

