【题目】二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:
①m=3;
②当∠APB=120°时,a= ![]() ;
;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥ ![]()
正确的是( )
A.①②
B.③④
C.①②③
D.①②③④
参考答案:
【答案】D
【解析】解:①∵点A(﹣m,0)、B(1,0)在抛物线y=ax2+bx+c上,
∴ ![]() ,
,
由①﹣②得
am2﹣bm﹣a﹣b=0,
即(m+1)(am﹣a﹣b)=0.
∵A(﹣m,0)与B(1,0)不重合,
∴﹣m≠1即m+1≠0,
∴m= ![]() ,
,
∴点C的坐标为(0,3a﹣3b),
∵点C在抛物线y=ax2+bx+c上,
∴c=3a﹣3b,
代入②得a+b+3a﹣3b=0,即b=2a,
∴m= ![]() =3,故①正确;
=3,故①正确;
②∵m=3,∵A(﹣3,0),
∴抛物线的解析式可设为y=a(x+3)(x﹣1),
则y=a(x2+2x﹣3)=a(x+1)2﹣4a,
∴顶点P的坐标为(﹣1,﹣4a).
根据对称性可得PA=PB,
∴∠PAB=∠PBA=30°.
设抛物线的对称轴与x轴的交点为G,
则有PG⊥x轴,
∴PG=AGtan∠PAG=2× ![]() =
= ![]() ,
,
∴4a= ![]() ,
,
∴a= ![]() ,故②正确;
,故②正确;
③在第一象限内作∠MBA=120°,且满足BM=BA,过点M作MH⊥x轴于H,如图1,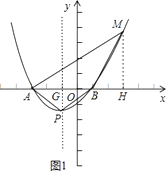
在Rt△MHB中,∠MBH=60°,
则有MH=4sin60°=4× ![]() =2
=2 ![]() ,BH=4cos60°=4×
,BH=4cos60°=4× ![]() =2,
=2,
∴点M的坐标为(3,2 ![]() ),
),
当x=3时,y= ![]() (3+3)(3﹣1)=2
(3+3)(3﹣1)=2 ![]() ,
,
∴点M在抛物线上,故③正确;
④∵点N在抛物线上,∴∠ABN≠90°,∠BAN≠90°.
当△ABN为直角三角形时,∠ANB=90°,
此时点N在以AB为直径的⊙G上,
因而点N在⊙G与抛物线的交点处,
要使点N存在,点P必须在⊙G上或⊙G外,如图2,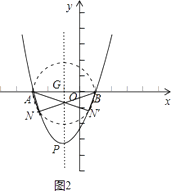
则有PG≥2,即4a≥2,也即a≥ ![]() ,故④正确.
,故④正确.
故选D.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把a、b中较小的数记作min{a,b},设函数f(x)={2
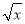 ,|x﹣2|}.若动直线y=m与函数y=f(x)的图象有三个交点,它们的横坐标分别为x1、x2、x3 , 则x1x2x3的最大值为________.
,|x﹣2|}.若动直线y=m与函数y=f(x)的图象有三个交点,它们的横坐标分别为x1、x2、x3 , 则x1x2x3的最大值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口
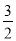 小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? 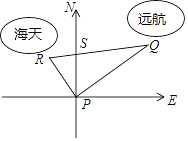
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,

求:(1)在图(1)中∠B+∠D=?(2)在图(2)中∠B+∠E1+∠D=?(3)在图(3)中∠B+∠E1+∠E2+…+∠En﹣1+∠En+∠D=?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4,设AB=x,AD=y,求x2+(y﹣4)2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图像如图所示.根据图像解答下列问题:
(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知l1∥l2,MN分别和直线l1、l2交于点A、B,ME分别和直线l1、l2交于点C、D,点P在MN上(P点与A、B、M三点不重合).
(1)如果点P在A、B两点之间运动时,∠α、∠β、∠γ之间有何数量关系请说明理由;
(2)如果点P在A、B两点外侧运动时,∠α、∠β、∠γ有何数量关系(只须写出结论).

相关试题

