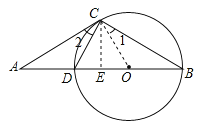
【题目】如图，点A是⊙O直径BD延长线上的一点，C在⊙O上，AC=BC，AD=CD．

（1）求证：AC是⊙O的切线；

（2）若⊙O的半径为2，求△ABC的面积．

参考答案：

【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）连接OC，根据等腰三角形的性质：等边对等角，以及直径所对的圆周角是直角，利用等量代换证得∠ACO=90°，据此即可证得；

（2）易证∠A=∠B=∠1=∠2=30°，即可求得AC的长，作CE⊥AB于点E，求得CE的长，利用三角形面积公式求解．

试题解析：（1）连接OC．∵AC=BC，AD=CD，OB=OC，∴∠A=∠B=∠1=∠2．∵∠ACO=∠DCO+∠2，∴∠ACO=∠DCO+∠1=∠BCD，又∵BD是直径，∴∠BCD=90°，∴∠ACO=90°，又C在⊙O上，∴AC是⊙O的切线；

（2）由题意可得△DCO是等腰三角形，∵∠CDO=∠A+∠2，∠DOC=∠B+∠1，∴∠CDO=∠DOC，即△DCO是等边三角形，∴∠A=∠B=∠1=∠2=30°，CD=AD=2，在直角△BCD中，BC===．又AC=BC，∴AC=．作CE⊥AB于点E．

在直角△BEC中，∠B=30°，∴CE=BC=，∴S△ABC=ABCE=×6×=．

关闭