【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN//y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;
(3)在(2)的条件下,是否存在m,使MN的长度最大?若存在,求m的值,幷求出此时点M和N的坐标;若不存在,说明理由.

参考答案:
【答案】(1)y=﹣x2+2x+3.(2) ﹣m2+3m(0<m<3).(3)m=1.5;M(1.5,1.5) N(1.5, ![]() )
)
【解析】试题分析:(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.
(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.
(3)通过配方即可求值.
试题解析:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:a(0+1)(0﹣3)=3,a=﹣1;∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.
(2)设直线BC的解析式为:y=kx+b,则有: ![]() ,解得
,解得![]() ;
;
故直线BC的解析式:y=﹣x+3.
已知点M的横坐标为m,则M(m,﹣m+3)、N(m,﹣m2+2m+3);
∴故N=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).
(3当m=-![]() =1.5时,MN的长度最大。
=1.5时,MN的长度最大。
当m=1.5时,-m+3=1.5
﹣m2+2m+3= ![]()
∴M(1.5,1.5) N(1.5, ![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2x2﹣18= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
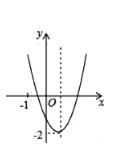
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上与表示-2的点相距5个单位长度的点所表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据1,2,3,0,﹣3,﹣2,﹣1的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合。
(1)旋转中心是 _________,旋转角为_____________度。
(2)请你判断△DFE的形状,并说明理由。
(3)求四边形DEBF的周长。

相关试题

