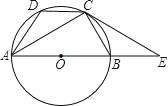
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.
(1)①填空:∠ACB= ,理由是 ;
②求证:CE与⊙O相切;
(2)若AB=6,CE=4,求AD的长.
参考答案:
【答案】(1)①90°;直径所对的圆周角是直角;②证明详见解析;(2)2.
【解析】
试题分析:(1)①根据圆周角定理即可求得;
②连接OC.欲证明CE是⊙O的切线,只需证明CE⊥OC即可;
(2)根据弦切角定理求得BE,进一步求得AC=4,得出△ACE和△BCE是等腰三角形,得出BC=BE=2,进一步证得∠DAB=∠ABC,从而证得AD=BC=2.
试题解析:①∵AB为⊙O的直径,
∴∠ACB=90°,
故答案为:90°;直径所对的圆周角是直角;
②连接OC,则∠CAO=∠ACO,
∵AC平分∠BAB,
∴∠BAC=∠CAD,
∵∠ECB=∠CAD.
∴∠BAC=∠ECB.
∴∠ECB=∠ACO,
∵∠ACO+∠OCB=90°,
∴∠ECB+∠OCB=90°,即CE⊥OC.
∴CE与⊙O相切;
(2)∵CE与⊙O相切,
∴![]() =BEAE,
=BEAE,
∵AB=6,CE=4,
∴![]() =BE(BE+6),
=BE(BE+6),
∴BE=2,
∴AE=6+2=8,
∵△ACE∽△CBE,
∴![]() ,即
,即![]() ,
,
∴AC=4,
∴AC=CE=4,
∴∠CAB=∠E,
∴∠ECB=∠E,
∴∠ABC=2∠ECB=2∠BAC,BC=BE=2,
∴∠DAB=∠ABC,
∴AD=BC=2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上与2距离为3个单位的点所表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的箱子里共有3个球,把它们的分别编号为1,2,3,这些球除编号不同外其余都相同,从箱子中随机摸出一个球,记录下编号后将它放回箱子,搅匀后再摸出一个球并记录下编号.
(1)用树状图或列表法举出所有可能出现的结果;
(2)求两次摸出的球都是编号为3的球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列哪种条件时,能判定△ABC与△DEF全等的是( )
A. ∠A=∠E, AB=EF, ∠B=∠D B. AB=DE, BC=EF, ∠C=∠F
C. AB=DE, BC=EF, ∠A=∠E, D. ∠A=∠D, AB=DE, ∠B=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图,先填空,然后回答问题.
(1)由上而下第8行,白球与黑球共有 个.
(2)若第n行白球与黑球的总数记作y,写出y与n的关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,然后解答提出的问题:
设a,b是有理数,且满足a+
 b=3﹣2
b=3﹣2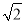 ,求ba的值.
,求ba的值.解:由题意得(a﹣3)+(b+2)
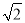 =0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
=0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,由于
 是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+
是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+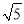 y=8+4
y=8+4 ,求x+y的值.
,求x+y的值. -
科目: 来源: 题型:
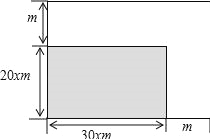
查看答案和解析>>【题目】如图,进行绿地的长、宽各增加xm.
(1)写出扩充后的绿地的面积y(
 )与x(m)之间的函数关系式;
)与x(m)之间的函数关系式;(2)若扩充后的绿地面积y是原矩形面积的2倍,求x的值.
相关试题

