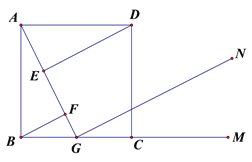
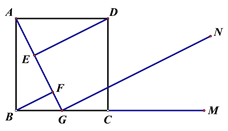
【题目】如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG。
参考答案:
【答案】(1)证明见解析;
(2)作图见解析,证明见解析.
【解析】解:∵ 四边形ABCD是正方形
∴ AB=BC=CD=DA
∠DAB=∠ABC=90°
 ∴ ∠DAE+∠GAB=90°
∴ ∠DAE+∠GAB=90°
∵ DE⊥AG BF⊥AG
∴ ∠AED=∠BFA=90°
∠DAE +∠ADE=90°
∴ ∠GAB =∠ADE
在△ABF和△DAE中
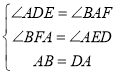
∴ △ABF≌△DAE
(2)作图略
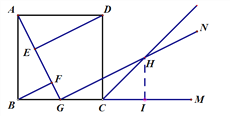 方法1:作HI⊥BM于点I
方法1:作HI⊥BM于点I
∵ GN∥DE
∴ ∠AGH=∠AED=90°
∴ ∠AGB+∠HGI=90°
∵ HI⊥BM
∴ ∠GHI+∠HGI=90°
∴ ∠AGB =∠GHI
∵ G是BC中点
∴ tan∠AGB=![]()
∴ tan∠GHI= tan∠AGB=![]()
∴ GI=2HI
∵ CH平分∠DCM
∴ ∠HCI=![]()
∴ CI=HI
∴ CI=CG=BG=HI
在△ABG和△GIH中
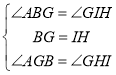
∴ △ABG≌△GIH
∴ AG=GH
-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的内角和是°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶.过了一段时间,汽车到达下一车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下图中近似地刻画出汽车在这段时间内的速度变化情况的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣2x+4的图象与x轴交点坐标是 , 与y轴交点坐标是 , 图象与坐标轴所围成的三角形面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M为线段AB的中点,C点将线段MB分成MC:CB=1:2的两部分,若MC=2,求线段AB的长.
从(l)、(2)中任选一道小题解答.
(1)认真阅读,理解题意,把解题过程补充完整:

解:因为MC:CB=1:2,MC=2.
所以CB=____
所以MB=____+____=6
因为M是AB中点,
所以AB=____ . MB=____
(2)若你有别的计算方法,也可以独立完成.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 两边及其中一边的对角分别相等的两个三角形全等
B. 两边及其中一边上的高分别相等的两个三角形全等
C. 有一直角边和一锐角分别相等的两个直角三角形全等
D. 面积相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x-5)(x+20)=x2+mx+n,则m=____.n=____.
相关试题

