【题目】阅读理解题
在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0(A2+B2≠0)的距离公式为:d=![]() ,
,
例如,求点P(1,3)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知:A=4,B=3,C=﹣3
所以P(1,3)到直线4x+3y﹣3=0的距离为:d=![]() =2
=2
根据以上材料,解决下列问题:
(1)求点P1(0,0)到直线3x﹣4y﹣5=0的距离.
(2)若点P2(1,0)到直线x+y+C=0的距离为![]() ,求实数C的值.
,求实数C的值.
参考答案:
【答案】(1)d=1;(2)C1=﹣3,C2=1.
【解析】
(1)根据点到直线的距离公式计算即可;
(2)根据点到直线的距离公式,列出方程即可解决问题.
解:(1)点P1(0,0)到直线3x﹣4y﹣5=0的距离:![]()
(2)![]()
∴|C+1|=2,
∴C+1=±2,
∴C1=﹣3,C2=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对[Q,R]的好点.
根据下列题意解答问题:
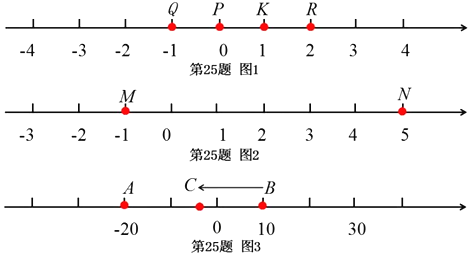
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R
表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是
有序点对
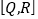 的好点,但点K不是有序点对
的好点,但点K不是有序点对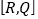 的好点.同理可以判断:
的好点.同理可以判断:点P__________有序点对
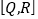 的好点,点R______________有序点对
的好点,点R______________有序点对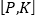 的好点(填“是”或“不是”);
的好点(填“是”或“不是”);(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,若点X是有序点对
 的好点,求点X所表示的数,并说明理由?
的好点,求点X所表示的数,并说明理由?(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从
点B出发,以每秒2个单位的速度向左运动t秒.当点A、B、C中恰有一个点为其余两有序点对的好点,求t的所有可能的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数
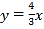 的图象的交于点C(m,4).
的图象的交于点C(m,4).(1)求m的值及一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标.
-
科目: 来源: 题型:
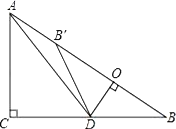
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】潮州市某学校为了改善办学条件,购置一批电子白板和台式电脑合共24台.经招投标,一台电子白板每台9000元,一台台式电脑每台3000元,设学校购买电子白板和台式电脑总费用为
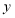 元,购买了
元,购买了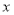 台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.(1)请求出
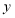 与
与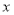 的函数解析式,并直接写出
的函数解析式,并直接写出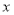 的取值范围
的取值范围(2)请问当购买多少台电子白板时,学校购置电子白板和台式电脑的总费用最少,最少多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
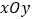 中,函数
中,函数 的图象与直线
的图象与直线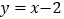 交于点
交于点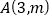 .
.(1)求
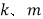 的值;
的值;(2)已知点
 ,过点
,过点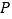 作平行于
作平行于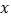 轴的直线,交直线
轴的直线,交直线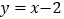 于点
于点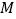 ,过点
,过点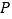 作平行于
作平行于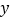 轴的直线,交函数
轴的直线,交函数 的图象于点
的图象于点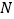 .
.①当
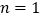 时,判断线段
时,判断线段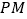 与
与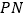 的数量关系,并说明理由;
的数量关系,并说明理由;②若
 ,结合函数的图象,直接写出
,结合函数的图象,直接写出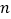 的取值范围.
的取值范围.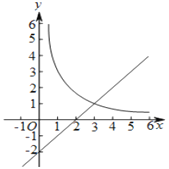
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在平面直角坐标系
 中,直线
中,直线 分别交
分别交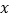 轴、
轴、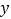 轴于点
轴于点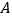 、
、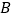 两点,直线
两点,直线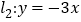 过原点且与直线
过原点且与直线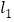 相交于
相交于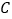 ,点
,点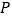 为
为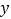 轴上一动点.
轴上一动点.(1)求点
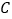 的坐标;
的坐标;(2)求出
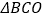 的面积;
的面积;(3)当
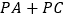 的值最小时,求此时点
的值最小时,求此时点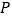 的坐标;
的坐标;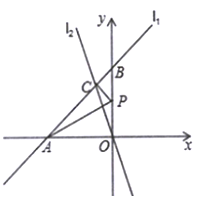
相关试题

