【题目】已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.

参考答案:
【答案】(1)①证明见解析;②证明见解析;(2)四边形PEFD是菱形.理由见解析.
【解析】试题分析:(1)①作PM⊥DG于M,根据等腰三角形的性质由PD=PG得MG=MD,根据矩形的判定易得四边形PCDM为矩形,则PC=MD,于是有DG=2PC;
②根据四边形ABCD为正方形得AD=AB,由四边形ABPM为矩形得AB=PM,则AD=PM,再利用等角的余角相等得到∠GDH=∠MPG,于是可根据“ASA”证明△ADF≌△MPG,得到DF=PG,加上PD=PG,得到DF=PD,然后利用旋转的性质得∠EPG=90°,PE=PG,所以PE=PD=DF,再利用DF⊥PG得到DF∥PE,于是可判断四边形PEFD为平行四边形,加上DF=PD,则可判断四边形PEFD为菱形;
(2)与(1)中②的证明方法一样可得到四边形PEFD为菱形.
试题解析:(1)①作PM⊥DG于M,如图1,

∵PD=PG,
∴MG=MD,
∵四边形ABCD为矩形,
∴PCDM为矩形,
∴PC=MD,
∴DG=2PC;
②∵四边形ABCD为正方形,
∴AD=AB,
∵四边形ABPM为矩形,
∴AB=PM,
∴AD=PM,
∵DF⊥PG,
∴∠DHG=90°,
∴∠GDH+∠DGH=90°,
∵∠MGP+∠MPG=90°,
∴∠GDH=∠MPG,
在△ADF和△MPG中,  ,
,
∴△ADF≌△MPG(ASA),
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF,
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形;
(2)解:四边形PEFD是菱形.理由如下:
作PM⊥DG于M,如图2,

与(1)一样同理可证得△ADF≌△MPG,
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】京沪高速公路全长1262千米,汽车沿京沪高速公路从上海驶往北京.
(1)那么汽车行驶全程所需时间t(小时)与行驶的平均速度v(千米/小时)之间有怎样的关系?t是v的什么函数?
(2)若平均速度为100千米/小时,大约需几个小时跑完全程?
(3)若跑完全程控制在10小时之内,那么车速应控制在什么范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店有单价为10元、15元和20元的三种文具盒出售,该商店统计了2014年3月份这三种文具盒的销售情况,并绘制统计图(不完整)如下:

(1)这次调查中一共抽取了多少个文具盒?
(2)求出图1中表示“15元”的扇形所占圆心角的度数;
(3)在图2中把条形统计图补充完整.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备
A型
B型
价格(万元/台)
m
m-3
月处理污水量(吨/台)
220
180
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点D3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形AnBnCnDn的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的曲线是函数y=
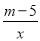 (m为常数)图象的一支.
(m为常数)图象的一支.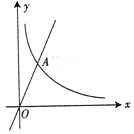
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
相关试题

