【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.

参考答案:
【答案】(1)∠ABE=55°;(2)证明见解析
【解析】试题分析:(1)由平行线的性质可求得∠ ABC =110°,由角平分线的定义可求得∠ABE=55°;(2)DF∥BE,理由:由AB∥ CD,根据平行线的性质可得∠A+∠ADC=180°,∠2=∠AFD,再由AD∥ BC,根据平行线的性质可得∠A+∠ABC=180°,所以∠ADC=∠ABC,再由∠1=∠2=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC,可得∠2=∠ABE,所以∠AFD =∠ABE,即可判定DF∥BE.
∠ABC,可得∠2=∠ABE,所以∠AFD =∠ABE,即可判定DF∥BE.
试题解析:
(1)解:∵AD∥BC,∠A=70°
∴∠ ABC=180°-∠ A=110°
∵BE平分∠ABC
∴∠ABE=![]() ∠ABC=55°
∠ABC=55°
(2)证明:DF∥BE
∵AB∥ CD
∴∠A+∠ADC=180°,∠2=∠AFD
∵AD∥ BC
∴∠A+∠ABC=180°
∴∠ADC=∠ABC
∵∠1=∠2=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC
∠ABC
∴∠2=∠ABE
∴∠AFD =∠ABE
∴DF∥BE
-
科目: 来源: 题型:
查看答案和解析>>【题目】-32x2y3的系数是 ________,次数是 ____________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的3条线段,能首尾依次相接组成三角形的是 ------------------ ( )
A. 1cm,2cm,4cm B. 8cm,6cm,4cm
C. 12cm,5cm,6cm D. 1cm,3cm,4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
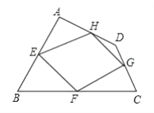
(1)四边形EFGH的形状是_________,证明你的结论;
(2)当四边形 ABCD的对角线满足_________条件时,四边形 EFGH是矩形;你学过的哪种特殊四边形的中点四边形是矩形? ________
(3)当四边形 ABCD的对角线满足_________条件时,四边形 EFGH是菱形;你学过
的哪种特殊四边形的中点四边形是菱形? _________.
-
科目: 来源: 题型:
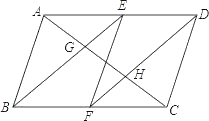
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
-
科目: 来源: 题型:
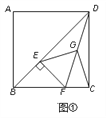
查看答案和解析>>【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG且EG⊥CG;
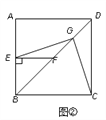
(2)将图①中△BEF绕B点逆时针旋转45,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
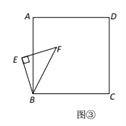
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=
 PQ D.AQ=4PQ
PQ D.AQ=4PQ
相关试题

